你也可以上程序咖(https://meta.chengxuka.com),打开大学幕题板块,不但有答案,讲解,还可以在线答题。
题目1:用筛选法求100 之内的素数。
解:
所谓"筛选法"指的是"埃拉托色尼(Eratosthenes)筛法"。埃拉托色尼是古希腊的著名数学家。他采取的方法是,在一张纸上写上1~1000 的全部整数,然后逐个判断它们是否是素数,找出一个非素数,就把它挖掉,最后剩下的就是素数,见图6.1。

具体做法如下∶
(1)先将1挖掉(因为1不是素数)。
(2)用2除它后面的各个数,把能被2整除的数挖掉,即把2的倍数挖掉。
(3)用3除它后面各数,把3 的倍数挖掉。
(4)分别用4,5…各数作为除数除这些数以后的各数。这个过程一直进行到在除数后面的数已全被挖掉为止。例如在图6.1中找1~50 的素数,要一直进行到除数为 47为止。事实上,可以简化,如果需要找1~n 的素数,只须进行到除数为 $ sqrt{n} $(取其整数)即可,例如对1~50,只须进行到将 $ sqrt{7} $ 作为除数即可。请读者思考为什么。
上面的算法可表示为∶
(1)挖去1;
(2)用下一个未被挖去的数 p 除 p 后面个数,把 p 的倍数挖掉;
(3)检查p是否小于 $ sqrt{n} $ 的整数部分(如果 n=1000,则检查 p<31 是否成立),如果是,则返回(2)继续执行,否则就结束;
(4)剩下的数就是素数。
用计算机解此题,可以定义一个数组 a。a[1]~a[n] 分别代表1~n这 n 个数。如果检查出数组 a的某一元素的值是非素数,就使它变为 0,最后剩下不为 0 的就是素数。
程序如下:
#include <stdio.h>
#include <math.h> //程序中用到求平方根函数 sqrt
int main()
{
int i, j, n, a[101]; //定义a数组包含101个元素
for (i = 1; i <= 100; i++) // a[0]不用,只用a[1]~a[100]
a[i] = i; //使 a[1]~a[100]的值为1~100
a[1] = 0; //先"挖掉"a[1]
for (i = 2; i < sqrt(100); i++)
for (j = i + 1; j <= 100; j++)
{
if (a[i] != 0 && a[j] != 0)
if (a[j] % a[i] == 0)
a[j] = 0; //把非素数“挖掉"
}
printf("
");
for (i = 2, n = 0; i <= 100; i++)
{
if (a[i] != 0) //选出值不为0的数组元素,即素数
{
printf("%5d", a[i]); //输出素数,宽度为5列
n++; //累积本行已输出的数据个数
}
if (n == 10)
{
printf("
");
n = 0;
}
}
printf("
");
return 0;
}
运行结果:

题目2:用选择法对10个整数排序。
解:
选择排序的思路为:设有10个元素 a[1]~a[10],将 a[1] 与 a[2]~a[10] 比较,若 a[1] 比 a[2]~a[10] 都小,则不进行交换,即无任何操作。若 a[2]~a[10] 中有一个以上比 a[1] 小,则将其中最大的一个(假设为 a[i] )与 a[1] 交换,此时 a[1] 中存放了10 个中最小的数。第 2 轮将 a[2] 与 a[3]~a[10] 比较,将剩下 9 个数中的最小者 a[i] 与 a[2] 对换,此时a[2] 中存放的是10 个中第二小的数。依此类推,共进行 9 轮比较,a[1]~a[10] 就已按由小到大的顺序存放了。N-S图如图6.2 所示。
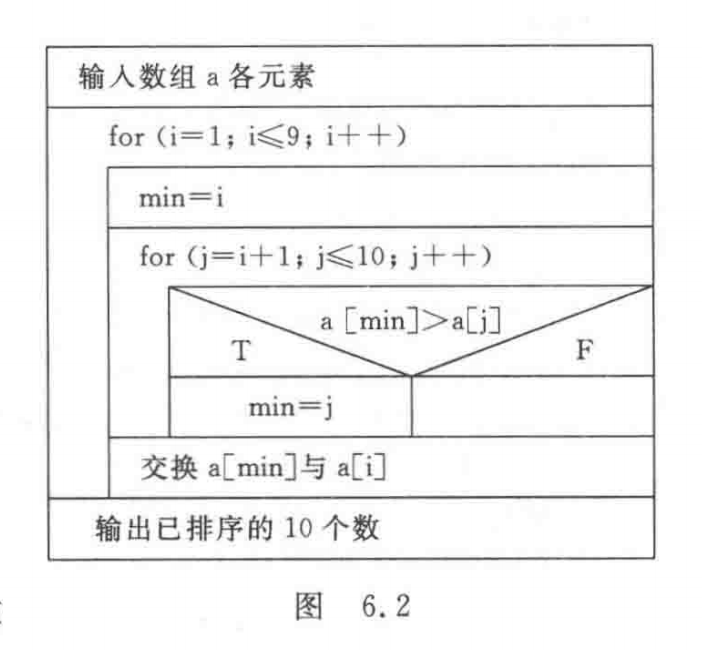
程序如下∶
#include <stdio.h>
int main()
{
int i, j, min, temp, a[11];
printf("enter data:
");
for (i = 1; i <= 10; i++)
{
printf("a[%d]=", i);
scanf("%d", &a[i]); //输人10个数
}
printf("
");
printf("The orginal numbers:
");
for (i = 1; i <= 10; i++)
printf("%5d", a[i]); //输出这10个数
printf("
");
for (i = 1; i <= 9; i++) //以下8行是对10个数排序
{
min = i;
for (j = i + 1; j <= 10; j++)
if (a[min] > a[j])
min = j;
temp = a[i]; //以下3行将a[i+ 1]~a[10]中的最小值与a[i]对换
a[i] = a[min];
a[min] = temp;
}
printf("
The sorted numbers:
"); //输出已排好序的10个数!
for (i = 1; i <= 10; i++)
printf("%5d", a[i]);
printf("
");
return 0;
}
运行结果:

输入10个数后,程序输出结果。
题目3:求一个 3×3 的整型矩阵对角线元素之和。
解:
答案代码:
#include <stdio.h>
int main()
{
int a[3][3], sum = 0;
int i, j;
printf("enter data:
");
for (i = 0; i < 3; i++)
for (j = 0; j < 3; j++)
scanf("%3d", &a[i][j]);
for (i = 0; i < 3; i++)
sum = sum + a[i][i];
printf("sum=%6d
", sum);
return 0;
}
运行结果:

关于输入数据方式的讨论:
在程序的 scanf 语句中用"%d"作为输入格式控制,上面输入数据的方式显然是可行的。其实也可以在一行中连续输入9个数据,如:

结果也一样。在输入完9个数据并按回车键后,这 9个数据被送到内存中的输入缓冲区中,然后逐个送到各个数组元素中。下面的输入方式也是正确的:

或者
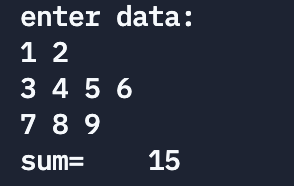
都是可以的。
请考虑,如果将程序第7~9行改为
for (j=0;j<3;j++)
scanf(" %d %d %d" , &a[0][j], &a[1][j],&a[2][j]);
应如何输入,是否必须一行输入3个数据,如:

答案是可以按此方式输入,也可以不按此方式输入,而采用前面介绍的方式输入,不论分多少行、每行包括几个数据,只要求最后输入完9个数据即可。
程序中用的是整型数组,运行结果是正确的。如果用的是实型数组,只须将程序第4 行的 int 改为 float 或 double 即可,在输入数据时可输入单精度或双精度的数。
题目4:有一个已排好序的数组,要求输入一个数后,按原来排序的规律将它插入数组中。
解:
假设数组 a有n个元素,而且已按升序排列,在插入一个数时按下面的方法处理:
(1)如果插入的数 num 比 a数组最后一个数大,则将插入的数放在 a数组末尾。
(2)如果插入的数 num不比a数组最后一个数大,则将它依次和 a[0]~a[n-1] 比较,直到出现 a[i] > num 为止,这时表示 a[0]~a[i-1] 各元素的值比 num 小,a[i] ~a[n-1] 各元素的值比 num 大。num理应插到 a[i-1] 之后、a[i] 之前。怎样才能实现此目的呢? 将 a[i]~a[n-1] 各元素向后移一个位置(即 a[i] 变成 a[i+1],…,a[n-1]变成 a[n] 。然后将 num 放在 a[i] 中。N-S图如图6.3所示。
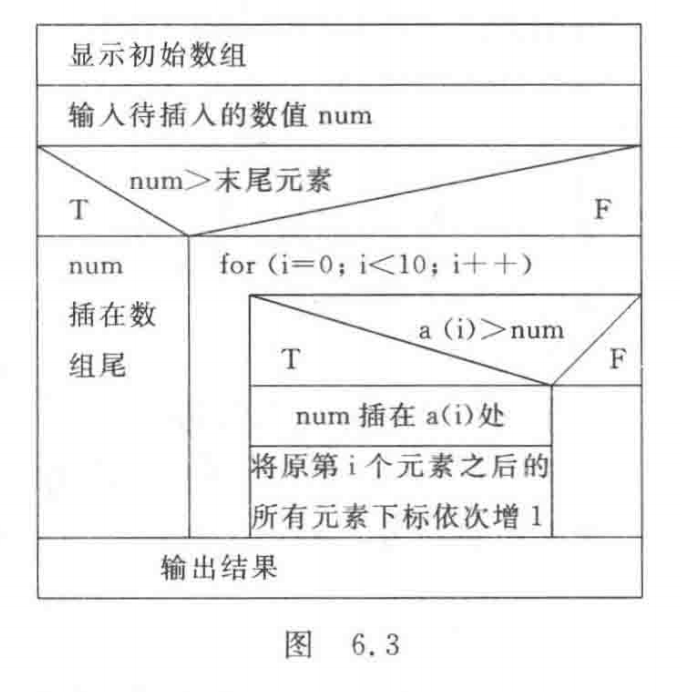
答案代码:
#include <stdio.h>
int main()
{
int a[11] = {1, 4, 6, 9, 13, 16, 19, 28, 40, 100};
int temp1, temp2, number, end, i, j;
printf("array a:
");
for (i = 0; i < 10; i++)
printf("%5d", a[i]);
printf("
");
printf("insert data:");
scanf("%d", &number);
end = a[9];
if (number > end)
a[10] = number;
else
{
for (i = 0; i < 10; i++)
{
if (a[i] > number)
{
temp1 = a[i];
a[i] = number;
for (j = i + 1; j < 11; j++)
{
temp2 = a[j];
a[j] = temp1;
temp1 = temp2;
}
break;
}
}
}
printf("Now aray a:
");
for (i = 0; i < 11; i++)
printf("%5d", a[i]);
printf("
");
return 0;
}
运行结果:

题目5:将一个数组中的值按逆序重新存放。例如,原来顺序为8,6,5,4,1。要求改为1,4,5,6,8。
解:
此题的思路是以中间的元素为中心,将其两侧对称的元素的值互换即可。 例如,将5和9互换,将8和6互换。N-S图见图6.4。

答案代码:
#include <stdio.h>
#define N 5
int main()
{
int a[N], i, temp;
printf("enter array a:
");
for (i = 0; i < N; i++)
scanf("%d", &a[i]);
printf("array a:
");
for (i = 0; i < N; i++)
printf("%4d", a[i]);
for (i = 0; i < N / 2; i++) //循环的作用是将对称的元素的值互换
{
temp = a[i];
a[i] = a[N - i - 1];
a[N - i - 1] = temp;
}
printf("
Now,array a:
");
for (i = 0; i < N; i++)
printf("%4d", a[i]);
printf("
");
return 0;
}
运行结果:

题目6:输出以下的杨辉三角形(要求输出 10行)
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
...
解:
杨辉三角形是 $ (a+b)^n $ 展开后各项的系数。例如:
$ (a+b)^0 $ 展开后为 1,系数为1
$ (a+b)^1 $ 展开后为 $ a+b $ ,系数为1,1
$ (a+b)^2 $ 展开后为 $ (a2+2ab+b2) $ ,系数为1,2,1
$ (a+b)^3 $ 展开后为 $ (a3+3a2b+3ab2+b3) $ ,系数为1,3,3,1
$ (a+b)^4 $ 展开后为 $ (a4+4a3b+6a2b2+4ab3+b4) $ ,系数为1,4,6,4,1
以上就是杨辉三角形的前5 行。杨辉三角形各行的系数有以下的规律∶
(1)各行第1个数都是1。
(2)各行最后一个数都是1。
(3)从第3行起,除上面指出的第1个数和最后一个数外,其余各数是上一行同列和前一列两个数之和。例如,第4行第 2个数(3)是第3行第2个数(2)和第3行第1个数(1)之和。可以这样表示∶
a[i][j]=a[i-1][j]+a[i-1]ij-1]
其中,i为行数,,为列数。
答案代码如下∶
#include <stdio.h>
#define N 10
int main()
{
int i, j, a[N][N]; //数组为10行10列
for (i = 0; i < N; i++)
{
a[i][i] = 1; //使对角线元素的值为1
a[i][0] = 1; //使第1列元素的值为1
}
for (i = 2; i < N; i++) //从第3 行开始处理
for (j = 1; j <= i - 1; j++)
a[i][j] = a[i - 1][j - 1] + a[i - 1][j];
for (i = 0; i < N; i++)
{
for (j = 0; j <= i; j++)
printf("%6d", a[i][j]); // 输出数组各元素的值
printf("
");
}
printf("
");
return 0;
}
说明:数组元素的序号是从 0 开始算的,因此数组中 0 行 0 列的元素实际上就是杨辉三角形中第 1 行第 1 列的数据,余类推。
运行结果:

题目7:输出"魔方阵"。所谓魔方阵是指这样的方阵,它的每一行、每一列和对角线之和均相等。例如,三阶魔方阵为
8 1 6
3 5 7
4 9 2
要求输出 1~n2 的自然数构成的魔方阵。
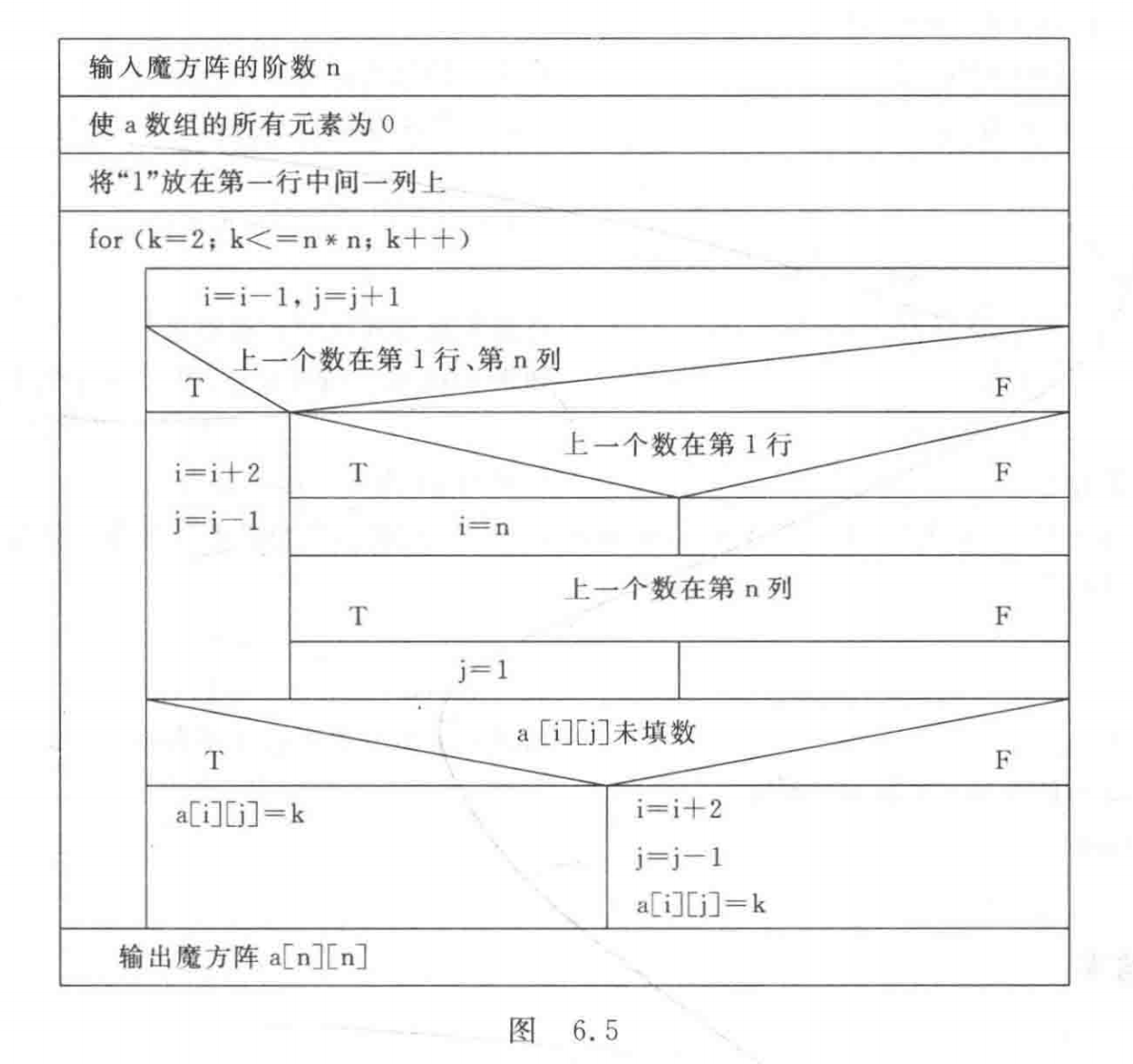
解:魔方阵中各数的排列规律如下∶
(1)将 1 放在第 1 行中间一列。
(2)从 2 开始直到 n×n 止,各数依次按此规则存放:每一个数存放的行比前一个数的行数减 1 ,列数加 1(例如上面的三阶魔方阵,5 在 4的上一行后一列)。
(3)如果上一数的行数为 1,则下一个数的行数为 n(指最下一行)。例如,1 在第 1 行,则 2 应放在最下一行,列数同样加 1。
(4)当上一个数的列数为 n 时,下一个数的列数应为 1,行数减 1。例如,2 在第 3 行最后一列,则 3 应放在第 2 行第 1 列。
(5)如果按上面规则确定的位置上已有数,或上一个数是第 1 行第 n 列时,则把下一个数放在上一个数的下面。例如,按上面的规定,4 应该放在第 1 行第 2 列,但该位置已被 1 占据,所以 4 就放在 3 的下面。由于 6 是第 1 行第 3 列(即最后一列),故 7 放在 6 下面。
按此方法可以得到任何阶的魔方阵。
N-S图如图6.5所示。
答案代码:
#include <stdio.h>
int main()
{
int a[15][15], i, j, k, p, n;
p = 1;
while (p == 1)
{
printf("enter n(n= 1--15) : "); //要求阶数为1~15 的奇数
scanf("%d", &n);
if ((n != 0) && (n <= 15) && (n % 2 != 0))
p = 0;
}
//初始化
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
a[i][j] = 0;
//建立魔方阵
j = n / 2 + 1;
a[1][j] = 1;
for (k = 2; k <= n * n; k++)
{
i = i - 1;
j = j + 1;
if ((i < 1) && (j > n))
{
i = i + 2;
j = j - 1;
}
else
{
if (i < 1)
i = n;
if (j > n)
j = 1;
}
if (a[i][j] == 0)
a[i][j] = k;
else
{
i = i + 2;
j = j - 1;
a[i][j] = k;
}
}
//输出魔方阵
for (i = 1; i <= n; i++)
{
for (j = 1; j <= n; j++)
printf("%5d", a[i][j]);
printf("
");
}
return 0;
}
说明:魔方阵的阶数应为奇数。
运行结果:

题目8:找出一个二维数组中的鞍点,即该位置上的元素在该行上最大、在该列上最小。也可能没有鞍点。
解:一个二维数组最多有一个鞍点,也可能没有。解题思路是∶先找出一行中值最大的元素,然后检查它是否为该列中的最小值,如果是,则是鞍点(不需要再找别的鞍点了),输出该鞍点; 如果不是,再找下一行的最大数……如果每一行的最大数都不是鞍点,则此数组无鞍点。
答案代码:
#include <stdio.h>
#define N 4
#define M 5 //数组为4行5列
int main()
{
int i, j, k, a[N][M], max, maxj, flag;
printf("please input matrix:
");
for (i = 0; i < N; i++) //输人数组
for (j = 0; j < M; j++)
scanf("%d", &a[i][j]);
for (i = 0; i < N; i++)
{
max = a[i][0]; //开始时假设 a[i][0]最大
maxj = 0; //将列号0赋给 maxj保存
for (j = 0; j < M; j++) //找出第i行中的最大数
if (a[i][j] > max)
{
max = a[i][j]; //将本行的最大数存放在max中
maxj = j; //将最大数所在的列号存放在 maxj中
}
flag = 1; //先假设是鞍点,以flag 为1代表
for (k = 0; k < N; k++)
if (max > a[k][maxj]) //将最大数和其同列元素相比
{
flag = 0; //如果 max不是同列最小,表示不是鞍点,令flag1为0
continue;
}
if (flag) //如果flagl为1表示是鞍点
{
printf("a[%d][%d]=%d
", i, maxj, max); //输出鞍点的值和所在行列号
break;
}
}
if (!flag) //如果 flag 为0表示鞍点不存在
printf("It is not exist!
");
return 0;
}
运行结果:
①

第 2~5行是输入的数据,最后一行是输出的结果。
②

(无鞍点)
题目9:有15个数按由大到小顺序存放在一个数组中,输入一个数,要求用折半查找法找出该数是数组中第几个元素的值。如果该数不在数组中,则输出"无此数"。
解:从表列中查一个数最简单的方法是从第 1 个数开始顺序查找,将要找的数与表列中的数一一比较,直到找到为止(如果表列中无此数,则应找到最后一个数,然后判定"找不到")。
但这种"顺序查找法"效率低,如果表列中有 1000个数,且要找的数恰恰是第 1000 个数,则要进行 999 次比较才能得到结果。平均比较次数为500次。
折半查找法是效率较高的一种方法。基本思路如下:
假如有已按由小到大排好序的9个数,a[1]~a[9],其值分别为
1,3,5,7,9,11,13,15,17
若输入一个数 3,想查 3 是否在此数列中,先找出表列中居中的数,即 a[5],将要找的数 3 与a[5] 比较,今[a5] 的值是 9,发现 a[5]>3,显然 3 应当在 a[1]~a[5]这部分,而不会在a[6]~a[9]这部分。这样就可以缩小查找范围,甩掉 a[6]~a[9] 这部分,即将查找范围缩小为一半。再找a[1]~a[5]的居中的数,即 a[3],将要找的数 3 与 a[3]比较,a[3]的值是 5,发现 a[3]>3,显然3应当在 a[1]~a[3]这部分。这样又将查找范围缩小一半。再将 3 与 a[1]~a[3] 的居中的数 a[2]比较,发现要找的数 3 等于 a[2],查找结束。一共比较了3 次。如果表列中有 n 个数,则最多比较的次数为 $ int(log_2n) +1 $ 。
N-S图如图6.6所示。

答案代码:
#include <stdio.h>
#define N 15
int main()
{
int i, number, top, bott, mid, loca, a[N], flag = 1, sign;
char c;
printf("enter data:
");
scanf("%d", &a[0]); //输入第1个数
i = 1;
while (i < N) //检查数是否已输入完毕
{
scanf("%d", &a[i]); //输入下一个数
if (a[i] >= a[i - 1]) //如果输人的数不小于前一个数
i++; //使数的序号加 1
else
printf("enter this data again:
"); //要求重新输入此数
}
printf("
");
for (i = 0; i < N; i++)
printf("%5d", a[i]); // 输出全部15个数
printf("
");
while (flag)
{
printf("input number to look for:"); //问你要查找哪个数
scanf("%d", &number); //输入要查找的数
sign = 0; // sign为0表示尚未找到
top = 0; // top 是查找区间的起始位置
bott = N - 1; // bott是查找区间的最末位置
if ((number < a[0]) || (number > a[N - 1])) //要查的数不在查找区间内
loca = -1; //表示找不到
while ((!sign) && (top <= bott))
{
mid = (bott + top) / 2; //找出中间元素的下标
if (number == a[mid]) //如果要查找的数正好等于中间元素
{
loca = mid; //记下该下标
printf("Has found %d,its position is %d
", number, loca + 1); //由于下标从0算起,而人们习惯从1算起,因此输出数的位置要加1
sign = 1; //表示找到了
}
else if (number < a[mid]) //如果要查找的数小于中间元素的值
bott = mid - 1; //只须在下标为0~mid-1的元素中找
else //如果要查找的数不小于中间元素的值
top = mid + 1;
} //只须在下标为 mid+1~bott的元素中找
if (!sign || loca == -1) // sign为0或 loca等于—1,意味着找不到
printf("cannot find %d.
", number); //输出"找不到"
printf("continue or not(Y/N)?"); //问你是否继续查找
scanf("%c", &c); //不想继续查找输入'N'或'n'
if (c == 'N' || c == 'n')
flag = 0; // lag 为开关变量.控制程序是否结束运行
}
return 0;
}
运行结果:
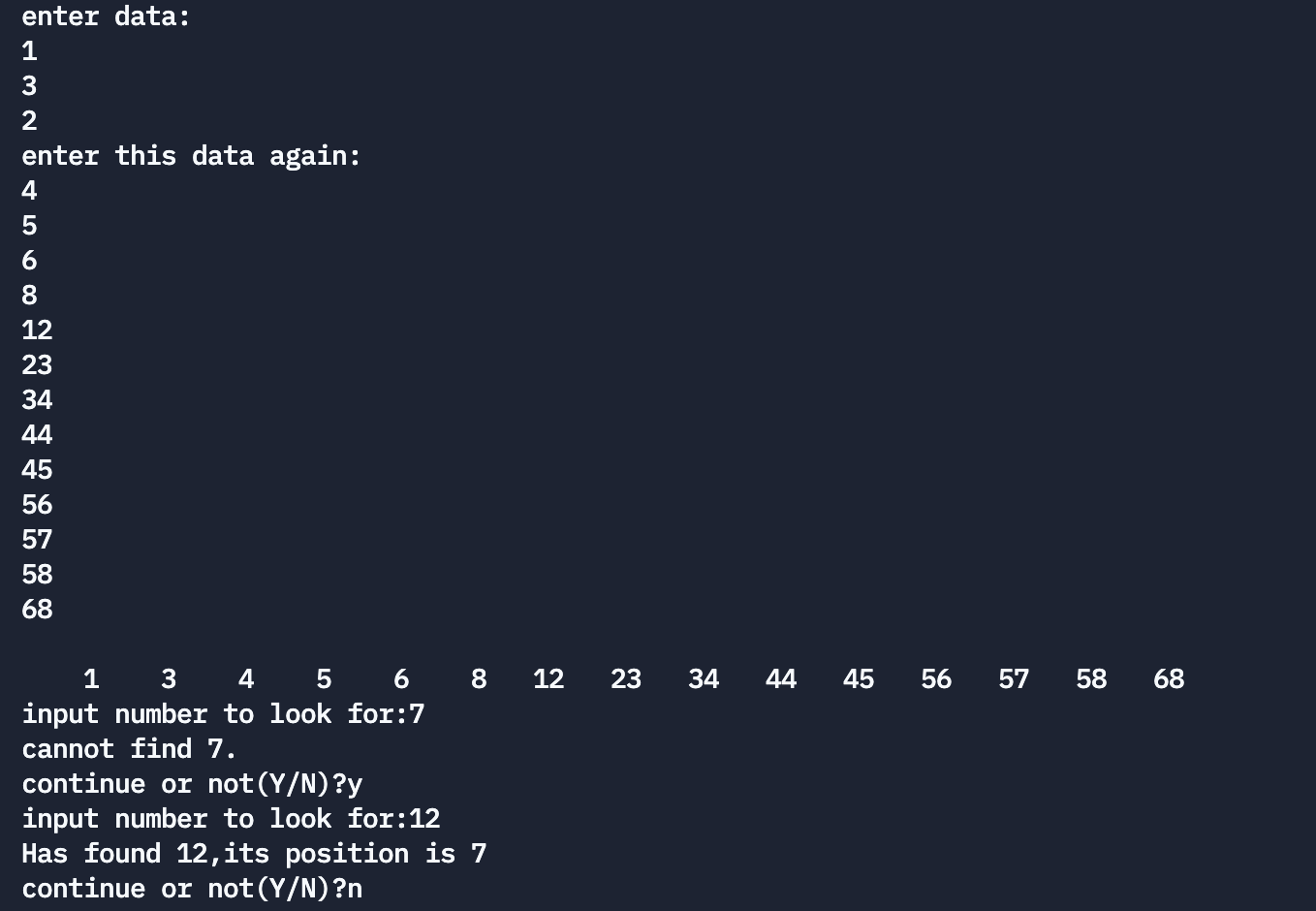
以上运行情况是这样的∶开始输入3 个数,由于顺序不是由小到大,程序不接收,要求重新输入。再输入15个数,然后程序输出这 15 个数,供核对。程序询问要找哪个数,输入7,输出"找不到7"。问是否继续找数,回答y表示 yes,再问找哪个数,输入12,输出"找到了。它是第7个数"。
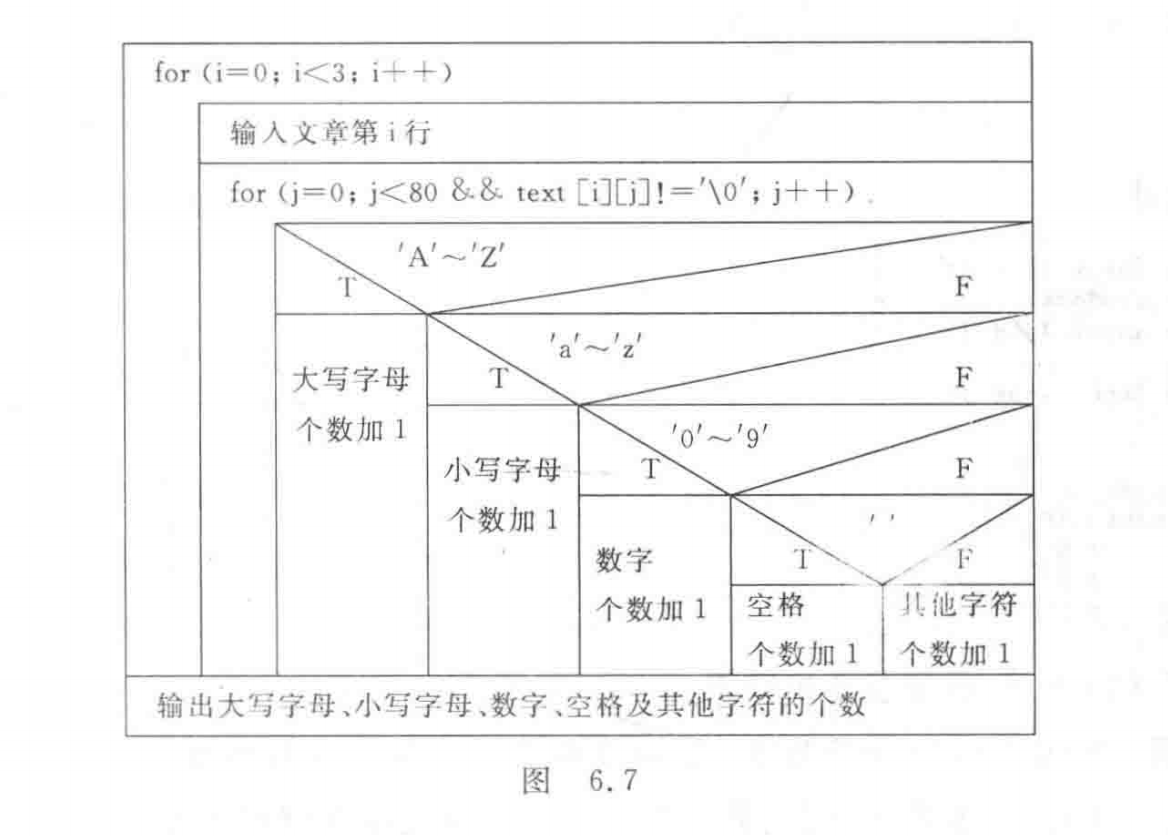
题目10:有一篇文章,共有3行文字,每行有 80个字符。要求分别统计出其中英文大写字母、小写字母、数字、空格以及其他字符的个数。
解:N-S图如图6.7所示。
答案代码:
#include <stdio.h>
int main()
{
int i, j, upp, low, dig, spa, oth;
char text[3][80];
upp = low = dig = spa = oth = 0;
for (i = 0; i < 3; i++)
{
printf("please input line %d:
", i + 1);
gets(text[i]);
for (j = 0; j < 80 && text[i][j] != '�'; j++)
{
if (text[i][j] >= 'A' && text[i][j] <= 'Z')
upp++;
else if (text[i][j] >= 'a' && text[i][j] <= 'z')
low++;
else if (text[i][j] >= '0' && text[i][j] <= '9')
dig++;
else if (text[i][j] == ' ')
spa++;
else
oth++;
}
}
printf("
");
printf("upper case :%d
", upp);
printf("lower case :%d
", low);
printf("digit :%d
", dig);
printf("space :%d
", spa);
printf("other :%d
", oth);
return 0;
}
运行结果:

先后输入了3行字符,程序统计出结果。
说明:数组 text 的行号为 0~2,但在提示用户输入各行数据时,要求用户输入第 1 行、第 2 行、第 3 行; 而不是第 0 行、第 1 行、第 2 行,这完全是照顾人们的习惯。为此,在程序第 6行中输出行数时用 i+1,而不用 i。这样并不影响程序对数组的处理,程序其他地方数组的第 1 个下标值仍然是 0~2。
题目11:输出以下图案
*****
*****
*****
*****
*****
解:
答案代码:
#include <stdio.h>
int main()
{
char a[5] = {'*', '*', '*', '*', '*'};
int i, j, k;
char space = ' ';
for (i = 0; i < 5; i++)
{
printf("
");
printf(" ");
for (j = 1; j <= i; j++)
printf("%c", space);
for (k = 0; k < 5; k++)
printf("%c", a[k]);
}
printf("
");
return 0;
}
运行结果:

题目12:有一行电文,已按下面规律译成密码∶
A→Z a→z
B→Y b→y
C→X c→x
....
即第1个字母变成第 26个字母,第 i个字母变成第(26-i+1)个字母,非字母字符不变。要求编程序将密码译回原文,并输出密码和原文。
解:可以定义一个数组 ch,在其中存放电文。如果字符 ch[j] 是大写字母,则它是 26个字母中的第(ch[j]-64)个大写字母。例如,若 ch[j] 的值是大写字母 'B',它的 ASCII 码为 66,它应是字母表中第(66-64)个大写字母,即第 2 个字母。按密码规定应将它转换为第(26-i+1)个大写字母,即第(26-2+1)= 25个大写字母。而 26-i+1=26 - (ch[j] - 64)+1=26+64-ch[j] + 1,即91-ch[j](如 ch[j] 等于 'B',91-'B'=91-66=25,ch[j] 应将它转换为第 25 个大写字母)。该字母的 ASCII 码为 91-ch[j] + 64,而91-ch[j] 的值 为 25,因此 91-ch[j]+64=25+64=89,89是 'Y' 的 ASCII 码。表达式 91-ch[i]+64 可以直接表示为155-ch[j] 。小写字母情况与此相似,但由于小写字母 'a' 的 ASCII 码为97,因此处理小写字母的公式应改为:26+96-ch[j]+1+96=123-ch[j]+96=219—ch[j] 。例如,若 ch[j] 的值为 'b',则其交换对象为 219—'b'=219—98=121,它是 'y' 的 ASCII 码。
由于此密码的规律是对称转换,即第 1个字母转换为最后一个字母,最后一个字母转换为第 1个字母,因此从原文译为密码和从密码译为原文,都是用同一个公式。
N-S图如图6.8所示。

答案代码:
(1)用两个字符数组分别存放原文和密码
#include <stdio.h>
int main()
{
int j, n;
char ch[80], tran[80];
printf("input cipher code:");
gets(ch);
printf("
cipher code :%s", ch);
j = 0;
while (ch[j] != '�')
{
if ((ch[j] >= 'A') && (ch[j] <= 'Z'))
tran[j] = 155 - ch[j];
else if ((ch[j] >= 'a') && (ch[j] <= 'z'))
tran[j] = 219 - ch[j];
else
tran[j] = ch[j];
j++;
}
n = j;
printf("
original text:");
for (j = 0; j < n; j++)
putchar(tran[j]);
printf("
");
return 0;
}
运行结果:

(2)只用一个字符数组
#include <stdio.h>
int main()
{
int j, n;
char ch[80];
printf("input cipher code:
");
gets(ch);
printf("
cipher code:%s
", ch);
j = 0;
while (ch[j] != '�')
{
if ((ch[j] >= 'A') && (ch[j] <= 'Z'))
ch[j] = 155 - ch[j];
else if ((ch[j] >= 'a') && (ch[j] <= 'z'))
ch[j] = 219 - ch[j];
else
ch[j] = ch[j];
j++;
}
n = j;
printf("original text:");
for (j = 0; j < n; j++)
putchar(ch[j]);
printf("
");
return 0;
}
运行结果:
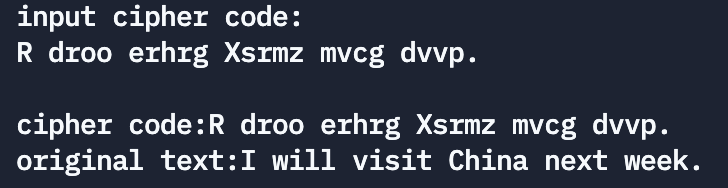
题目13:编一程序,将两个字符串连接起来,不要用strcat 函数。
解:
N-S图如图6.9所示。

答案代码:
#include <stdio.h>
int main()
{
char s1[80], s2[40];
int i = 0, j = 0;
printf("input string1:");
scanf("%s", s1);
printf("input string2:");
scanf("%s", s2);
while (s1[i] != '�')
i++;
while (s2[j] != '�')
s1[i++] = s2[j++];
s1[i] = '�';
printf("
The new string is :%s
", s1);
return 0;
}
运行结果:
题目14:编一个程序,将两个字符串sl和s2 比较,若s1>s2,输出一个正数; 若s1=s2.输出0;若sl<s2,输出一个负数。不要用 strcpy 函数。两个字符串用gets 函数读入。输出的正数或负数的绝对值应是相比较的两个字符串相应字符的 ASCII码的差值。例如,"A"与"C"相比,由于"A"<"C",应输出负数,同时由于'A'与'C'的 ASCII码差值为2,因此应输出"-2"。同理∶"And"和"Aid"比较,根据第2个字符比较结果,"n"比"i"大5,因此应输出"5"。
解:
#include <stdio.h>
int main()
{
int i, resu;
char s1[100], s2[100];
printf("input string1:");
gets(s1);
printf("
input string2:");
gets(s2);
i = 0;
while ((s1[i] == s2[i]) && (s1[i] != '�'))
i++;
if (s1[i] == '�' && s2[i] == '�')
resu = 0;
else
resu = s1[i] - s2[i];
printf("
result:%d.
", resu);
return 0;
}
运行结果:
题目15:编写一个程序,将字符数组 s2 中的全部字符复制到字符数组 s1中。不用strcpy 函数。复制时,�'也要复制过去。�'后面的字符不复制。
解:
#include <stdio.h>
int main()
{
char s1[80], s2[80];
int i;
printf("input s2:");
scanf("%s", s2);
for (i = 0; i <= strlen(s2); i++)
s1[i] = s2[i];
printf("s1:%s
", s1);
return 0;
}
运行结果:
本文摘自 :https://www.cnblogs.com/

