预处理欧拉函数

预处理欧拉函数
2022-09-06 22:51:51

1、AcWing基础课：

线性筛：（与线性筛质数对应）

    phi[1] = 1;
    for (int i = 2; i <= n; i ++) 
    {
        if (!st[i]) 
        {
            primes[cnt ++] = i;
            phi[i] = i - 1;
        }
        for (int j = 0; primes[j] <= n / i; j ++)
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0)
            {
                phi[primes[j] * i] = phi[i] * primes[j];
                break;
            }
            phi[primes[j] * i] = phi[i] * (primes[j] - 1);
        }
    }

View Code

证明：

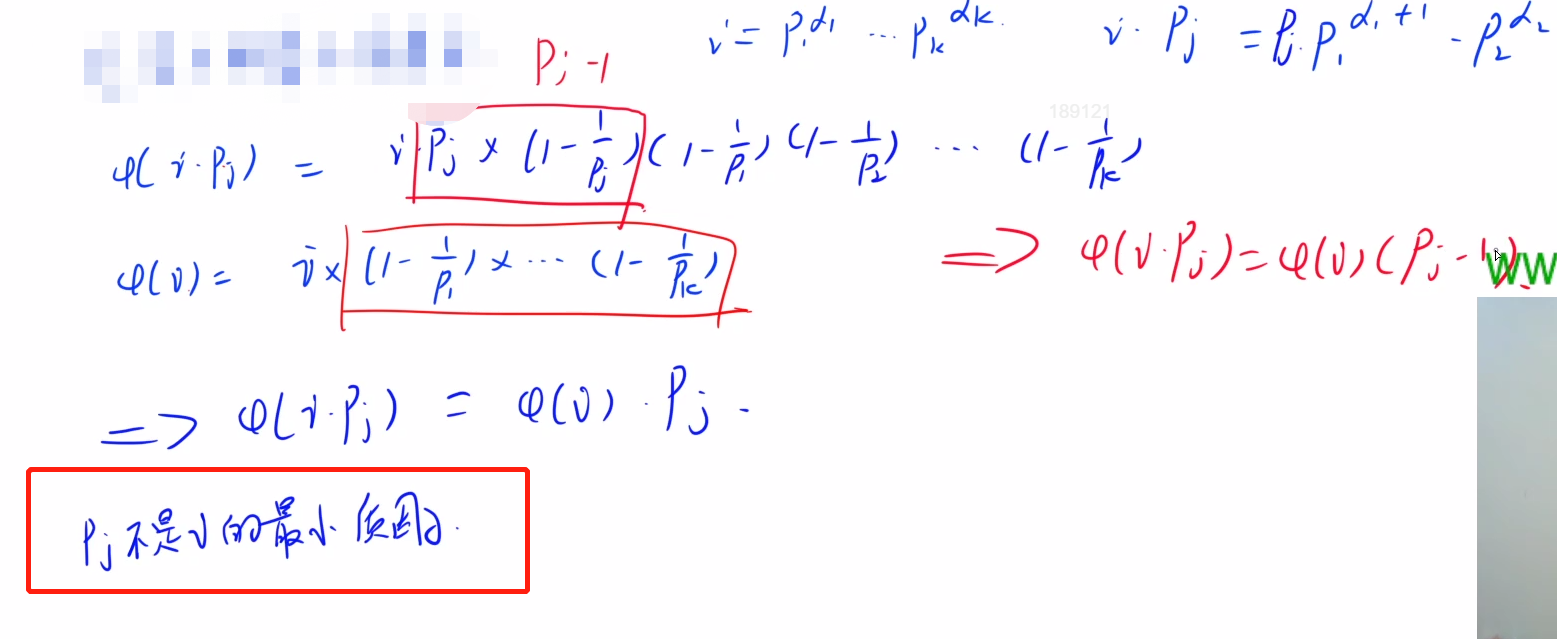
2、参考：https://www.bilibili.com/video/BV1MK411f7RW?spm_id_from=333.337.search-card.all.click&vd_source=75ae018f8d1181302d7ea76b60c928f4

nloglogn筛：（贡献度思想，与埃氏筛对应）

    for (int i = 1; i <= n; i++)
        phi[i] = i;
    for (int i = 2; i <= n; i++)
    {
        if (phi[i] == i)
        {
            for (int j = i; j <= n; j += i)
            {
                phi[j] = phi[j] / i * (i - 1);
            }
        }
    }

View Code

这里可以对应欧拉函数的求法：

“

欧拉函数的定义是，φ(n)是1-n中与n互质的数的个数

对n分解质因数得p1^a1*p2^a2*...*pn^an，

则φ(n)=n*(1-1/p1)(1-1/p2)*...*(1-1/pn);

”

初始化phi[i]=i，

如果没有筛到，则确认为质数，然后将此质数p的倍数的phi，phi=phi/p*(p-1)

本文摘自：https://www.cnblogs.com/

开通会员，享受整站包年服务立即开通 >

预处理欧拉函数2022-09-06 22:51:51

预处理欧拉函数
2022-09-06 22:51:51