
Hello,大家好我叫是Dream呀,一个有趣的Python博主,小白一枚,多多关照 ?
入门须知:这片乐园从不缺乏天才,努力才是你的最终入场券!
最后,愿我们都能在看不到的地方闪闪发光,一起加油进步
“一万次悲伤,依然会有Dream,我一直在最温暖的地方等你”,唱的就是我!哈哈哈~
第一章算法简介:
- 1.1引言
1.1引言
算法是一组完成任务的指令,任何代码片段都可以看做是一个算法!
1.1.1性能方面
本专栏介绍的每种算法都很可能有使用你喜欢的语言编写实现,你将学习到不同算法的优缺点,进而选择更好地算法!
1.1.2问题解决及技巧
利用这些广泛的算法,你将会学习到更具体的AI算法,数据库算法。
1.2 二分查找
二分查找是一种算法,其输入必须是一个有序的元素列表。如果要查找的元素包含在列表中,二分查找返回其位置;否则返回null。
1.2.1简单查找
依次查找n次,又叫做傻找
1.2.2更佳的查找方式
每次从中间开始查找,就是我们所说的二分查找,这样我们的时间复杂度就是logn,而不是简单查找中的n

def binary_search(list,item):
low=0
high=len(list)-1
while low<=high:
mid=(low+high)//2
guess=list[mid]
if guess==item:
return mid
if guess>item:
high=mid-1
else:
low=mid+1
return None
print(binary_search([1,3,5,7],1))
1.2.3运行时间
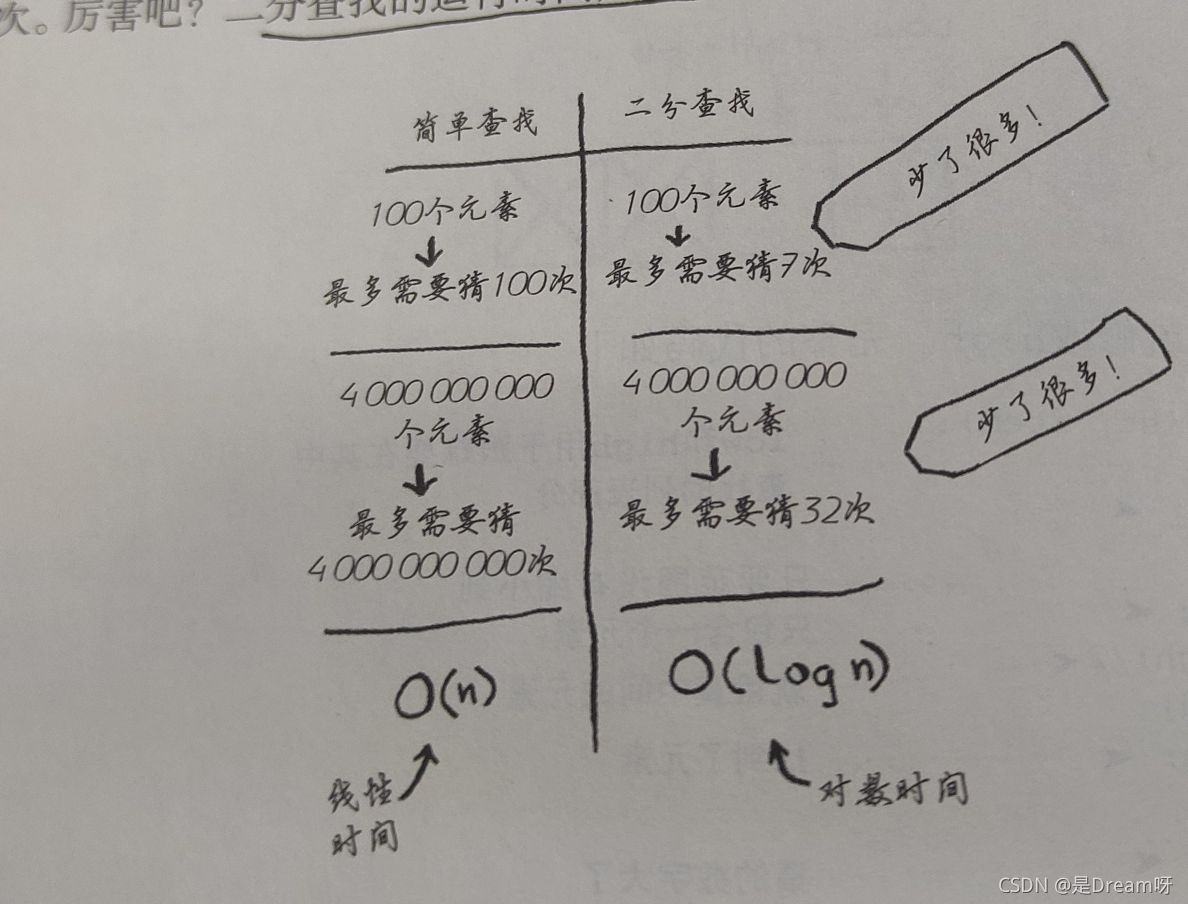
如果有100个元素,简单查找需要找100次;而如果有40个亿的元素,其更是要查找40亿次,先不说时间问题,估计你的电脑跑出来这个程序也离退休不远了~
换而言之,这种时间被称为线性时间。
二分查找则不同,100个元素只需要7次;40亿个元素,只需要惊人的32次!
这样的运行时间被称为对数时间。
1.3大O表示法
大O表示法是一种特殊的表示法,指出了算法有多快。
1.3.1算法的运行时间以不同的速度增加
例如:为检查长度为的的列表,简单查找需要查找n次,运行时间为O(n),二分查找的运行时间为O(log n)。这指出了算法需要执行的操作数。之所以被称为大O表示法,是因为操作数前面有个O。这听起来像笑话,但事实确实如此。
1.3.2 理解不同的大O运算时间
大O表示法指出了最糟糕的情况下的运行时间。
1.3.3一些常见的大O运行时间
- O(log n):对数时间,这样的算法包括二分查找
- O(n):线性时间,这样的算法包括简单查找
- O(n*log n):这样的算法包括快速排序
- O(n**2):这样的算法包括选择排序
- O(n!):这样的算法包括旅行商问题的解决方案

注意:
1.算法的速度并非指时间,而是操作数的增速
2.谈论算法的速度时,我们说的是随着输入的增加,其运行时间将以什么样的速度增加
3.算法的运行时间用大O表示法表示
4.O(logn)比O(n)快,当需要搜索的元素越多时,前者比后者快得多。
1.3.4旅行商
一位商人要去往五个城市,规划出最优路线。这需要我们先找出所有路线再作比对,也就是5!,这个方法很费时间,但目前还没有找到更快的算法。
1.4小结
1.二分查找的速度比简单查找快得多
2.O(log n)比O(n)快,需要搜索的元素越多,前者比后者就更快得多!
3.算法运行时间不是以秒为单位
4.算法运行时间是从其增速的角度度量的
5.算法运行时间用大O表示法表示
最后的福利
最后一点小福利带给大家:如果想快速上手python的小伙伴们,这个详细整理PPT可以迅速帮助大家打牢python基础,需要的小伙伴们可以下载一下Python入门基础教程全套+小白速成+学不会来找我!
好啦,这就是今天要给大家分享的全部内容了
如果你喜欢的话,就不要吝惜你的一键三连了~
本文摘自 :https://blog.51cto.com/u

