
Hello,大家好我叫是Dream呀,一个有趣的Python博主,小白一枚,多多关照 ?
入门须知:这片乐园从不缺乏天才,努力才是你的最终入场券!
最后,愿我们都能在看不到的地方闪闪发光,一起加油进步
“一万次悲伤,依然会有Dream,我一直在最温暖的地方等你”,唱的就是我!哈哈哈~
第一章 线性空间
- 一、向量
- 二、向量组
- 三、矩阵
1.1线性代数知识回顾
一、向量
1、向量的实际意义
确定飞机的状态,需要以下6个
参数:
飞机重心在空间的位置参数 P(x,y,z)
机身的水平转角:
a
机身的仰角:
b
机翼的转角;
c
所以,确定飞机的状态,需用6维向量
a = (x, y,z,a,b ,c )
确定西瓜是好瓜还是坏瓜? 需要描述西瓜的特征
如下:
颜色:深绿、浅绿、浅白
根蒂:硬挺、稍卷
条纹:清晰、模糊
糖分:连续的值
西瓜:(深绿, 硬挺,清晰,1.2)
2、向量的线性运算
3、向量的内积

4、向量的长度

二、向量组
1、向量组的实际意义
利用如下特征描述一车西瓜的特点,确定一车西瓜哪些是好瓜,哪些是坏瓜?
一车西瓜有若干个向量表示,构成向量组。
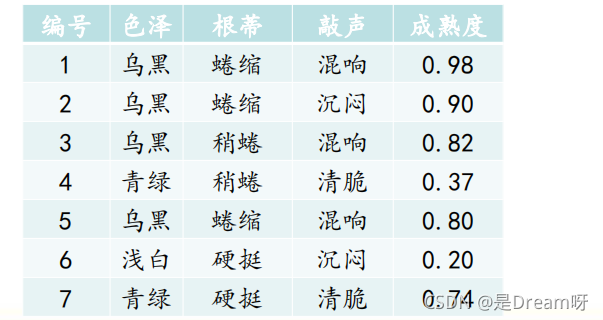
2、向量的线性表示

3、向量组的线性相关

4、向量组的线性无关

一个零向量线性相关,而一个非零向量线性无关
5、向量组的极大无关组
定义:设向量组 A 与其一个部分向量组A0:a1, a2, …, ar,如果满足:
① 向量组A0:a1, a2, …, ar线性无关;
② 向量组 A中任意一个向量都能由向量组 A0 线性表示;
那么称向量组 A0是向量组A的一个极大线性无关组,简称极大无关组
6、向量组的秩
定义:向量组的极大无关组所含向量的个数,记作r(A)
三、矩阵
1.矩阵的意义

2、特殊矩阵

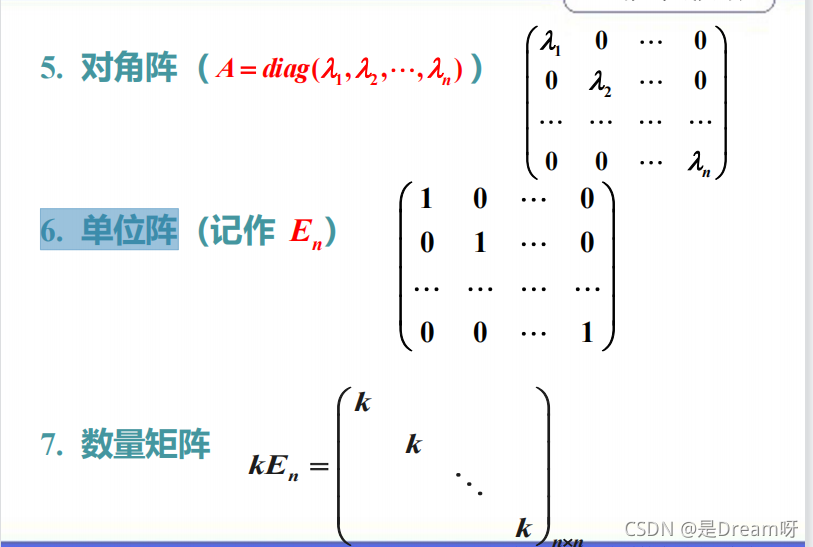
8.三角矩阵
3、 矩阵的运算
(1) 加、减
(2) 数乘
(3) 乘法
注意:
矩阵乘法不满足交换律;
矩阵乘法不满足消去律
两个非零矩阵的乘法可能是零矩阵
(4)逆矩阵的概念


4、矩阵秩的计算
定义:矩阵A 的最高阶非零子式的阶数, 称为矩阵,A 的秩,记作 r(A).
r(A)=2
- 存在一个非零二阶子式
- 所有的三阶及以上子式都等于0
r(A)=r
- 存在一个非零r阶子式
- 所有的r+1阶及以上子式都等于0
规定:零矩阵的秩等于零.
求矩阵的秩的方法:
(1) 化行阶梯形矩阵;
(2) 行阶梯形矩阵中非零行的行数
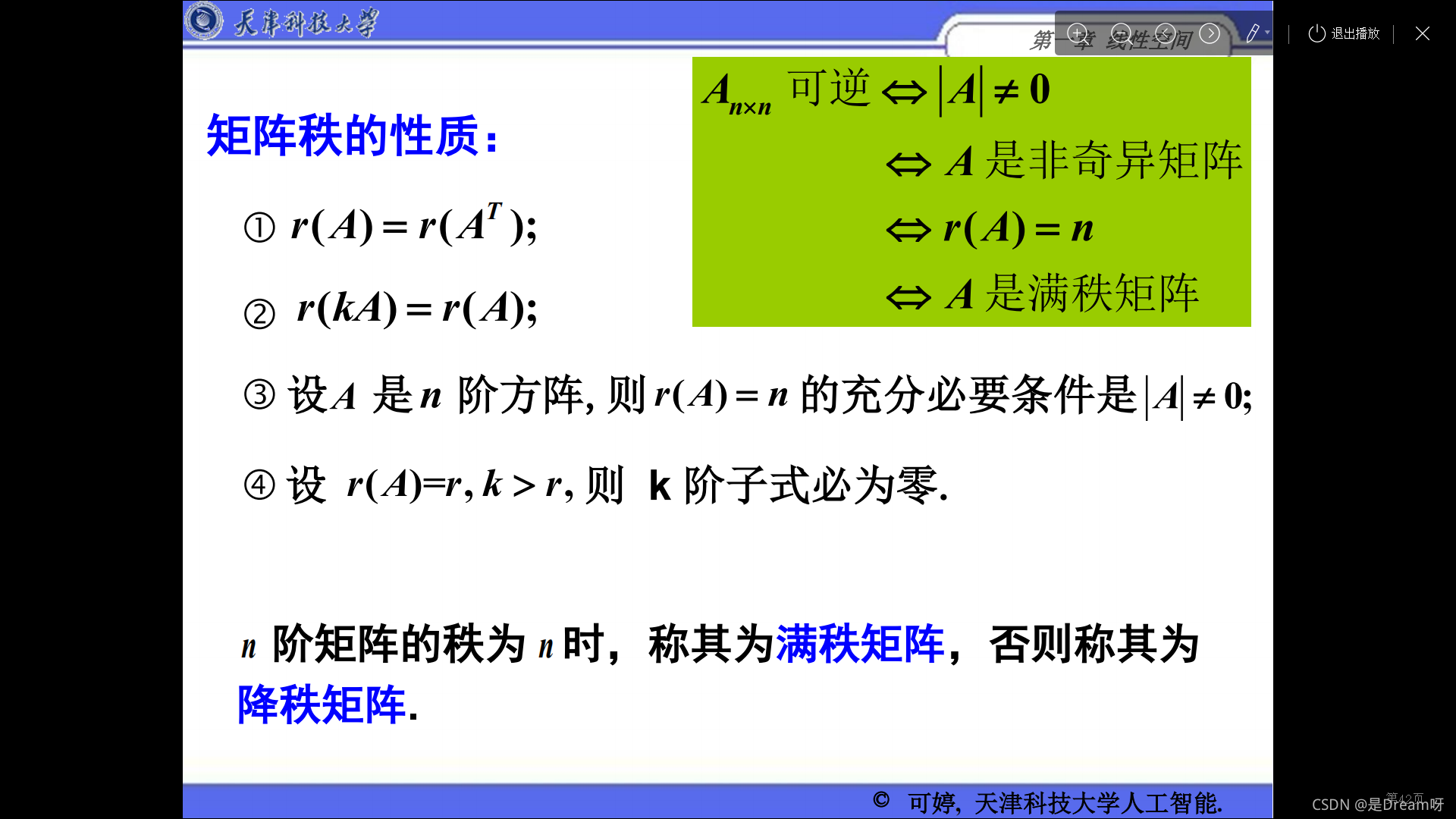
n阶矩阵的秩为n时,称其为满秩矩阵,否则称其为降秩矩阵.
四、线性方程组
1.向量、矩阵与线性方程组的关系
- 向量组构成矩阵
- 用向量组的线性组合表示方程组
- 矩阵可以表示线性方程组
- 向量组的秩=矩阵的秩=有效方程的个数

2.线性方程组解的判定(利用矩阵的秩讨论)
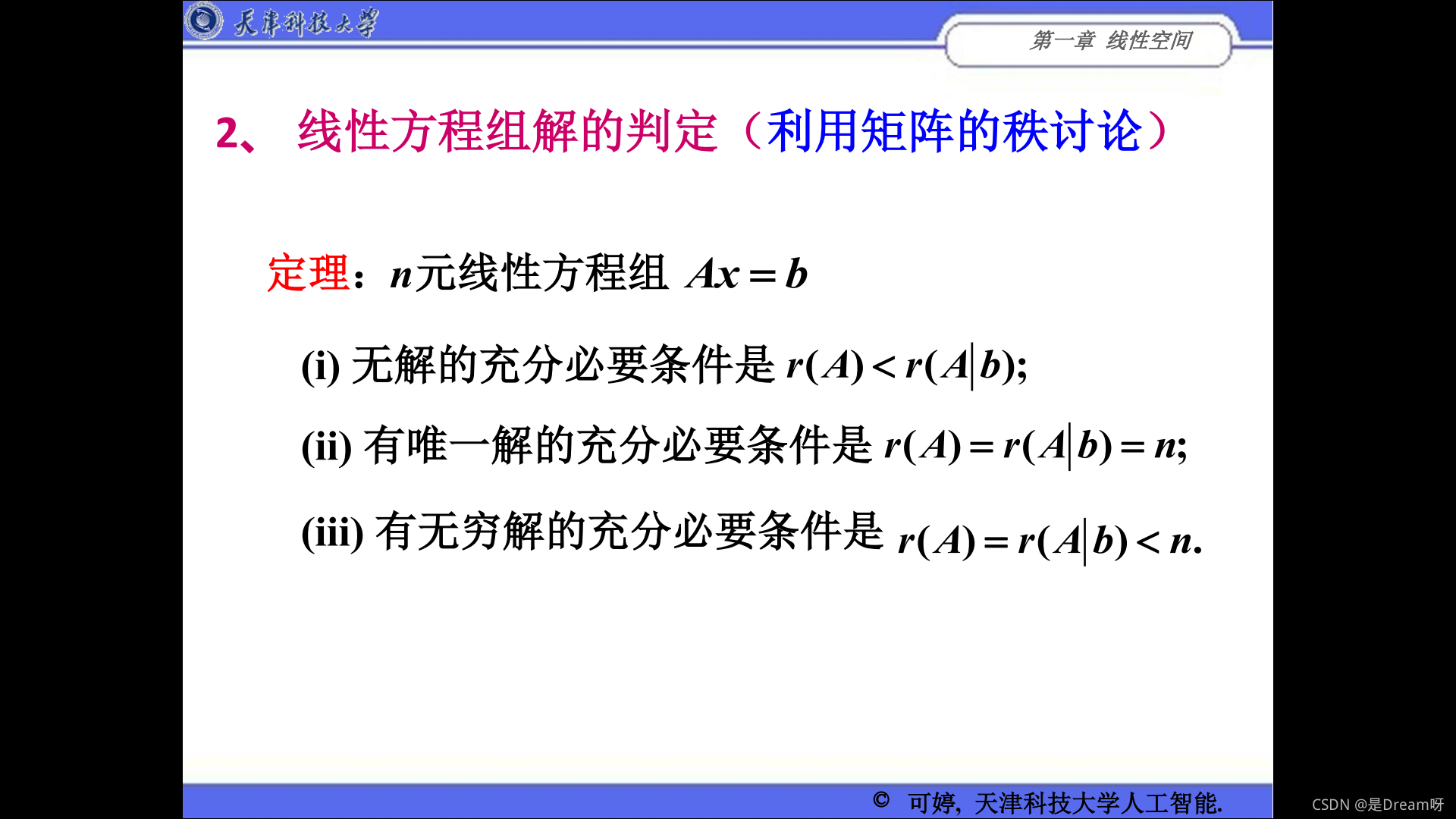
3、 齐次线性方程组的解法

4、 线性方程组的应用
1.2 线性空间
一、数域
封闭:指集合中任意两个元素作某一运算得到的结果仍属于该集合.
数域:数集关于四则运算是封闭的
二、向量空间
定义:设 V 是 一个向量组集合,如果
① 集合 V 非空,
② 集合 V 对于向量的加法和数乘两种运算封闭,具体地说,就是:
- ✓ 若 a ∈ V, b ∈ V,则 a + b ∈ V .(对加法封闭)
- ✓ 若 a ∈ V, l ∈ R,则 l a ∈ V . (对数乘封闭)
那么就称集合 V 为向量空间.
齐次线性方程组的解集 S1 = { x | Ax = 0 }是向量空间
定义:齐次线性方程组的解集称为齐次线性方程组的解空间

向量空间的基和维数
基:向量组的一个极大无关组
维数:向量组的秩
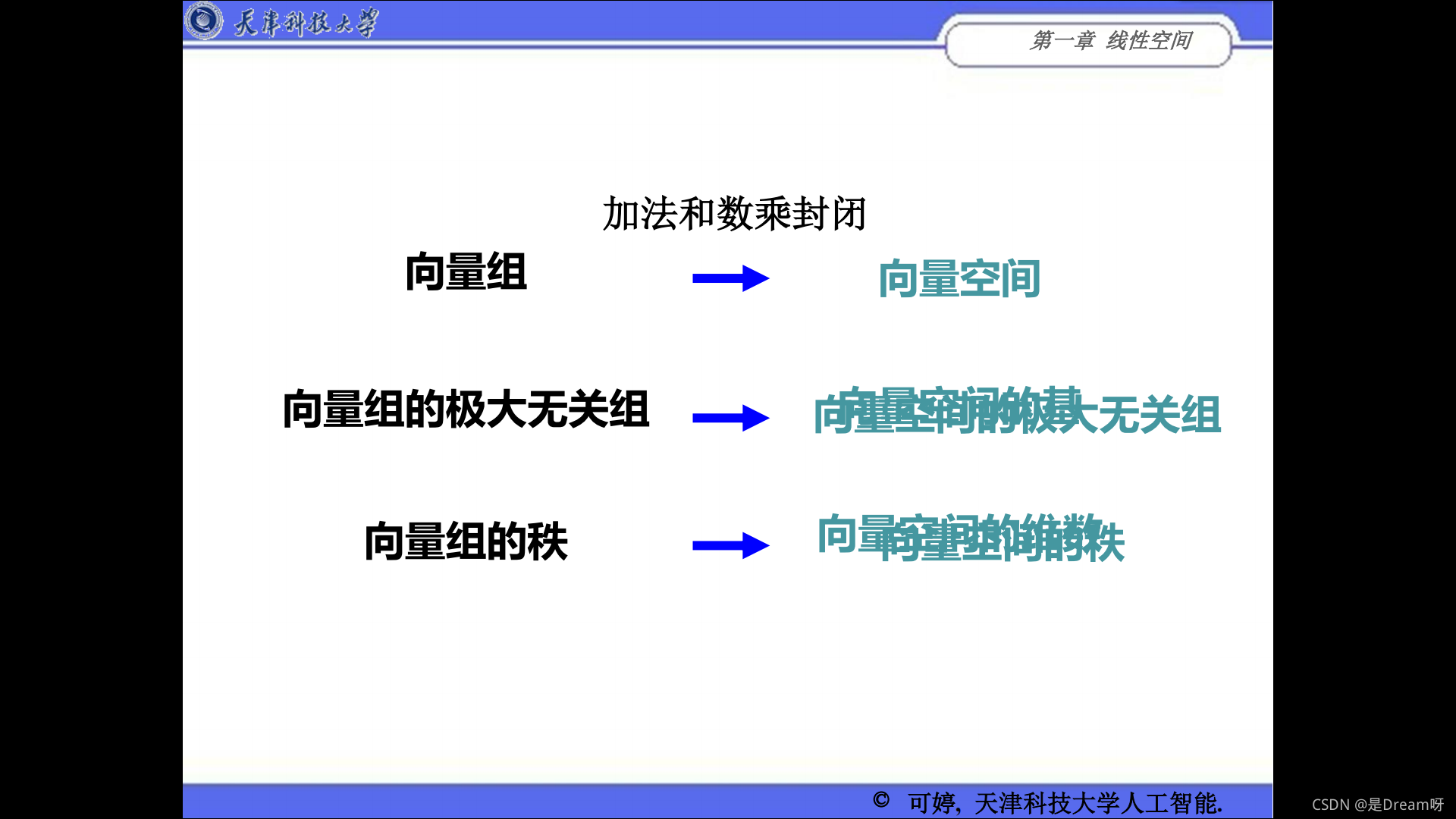
三、线性空间

四、 线性空间的基与维数

五、线性子空间
定义:如果线性空间 V 的非空子集合 V1 对于 V 中所定义的
加法及乘数两种运算是封闭的,则称 V1 是 V 的子空间.
平凡子空间:零空间,V本身
例:
- 1.n 维向量的全体Rn (1) 集合 V1 = { (0, x2, …, xn)T | x2, …, xn∈R }
- 2. 集合 V2 = { (1, x2, …, xn)T | x2, …, xn∈R } 解:V1 是 Rn 的子空间, V2 不是 Rn
的子空间

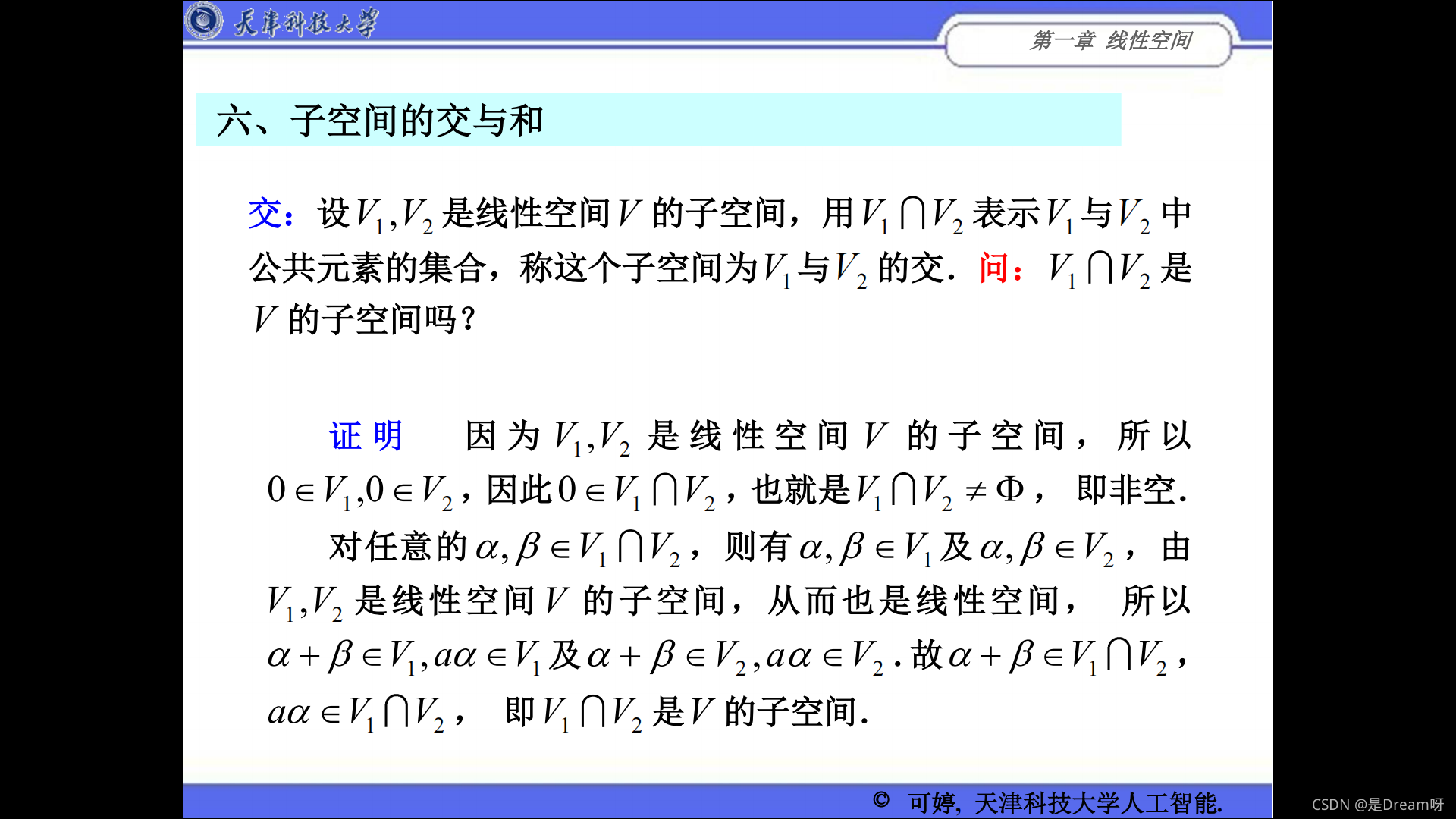
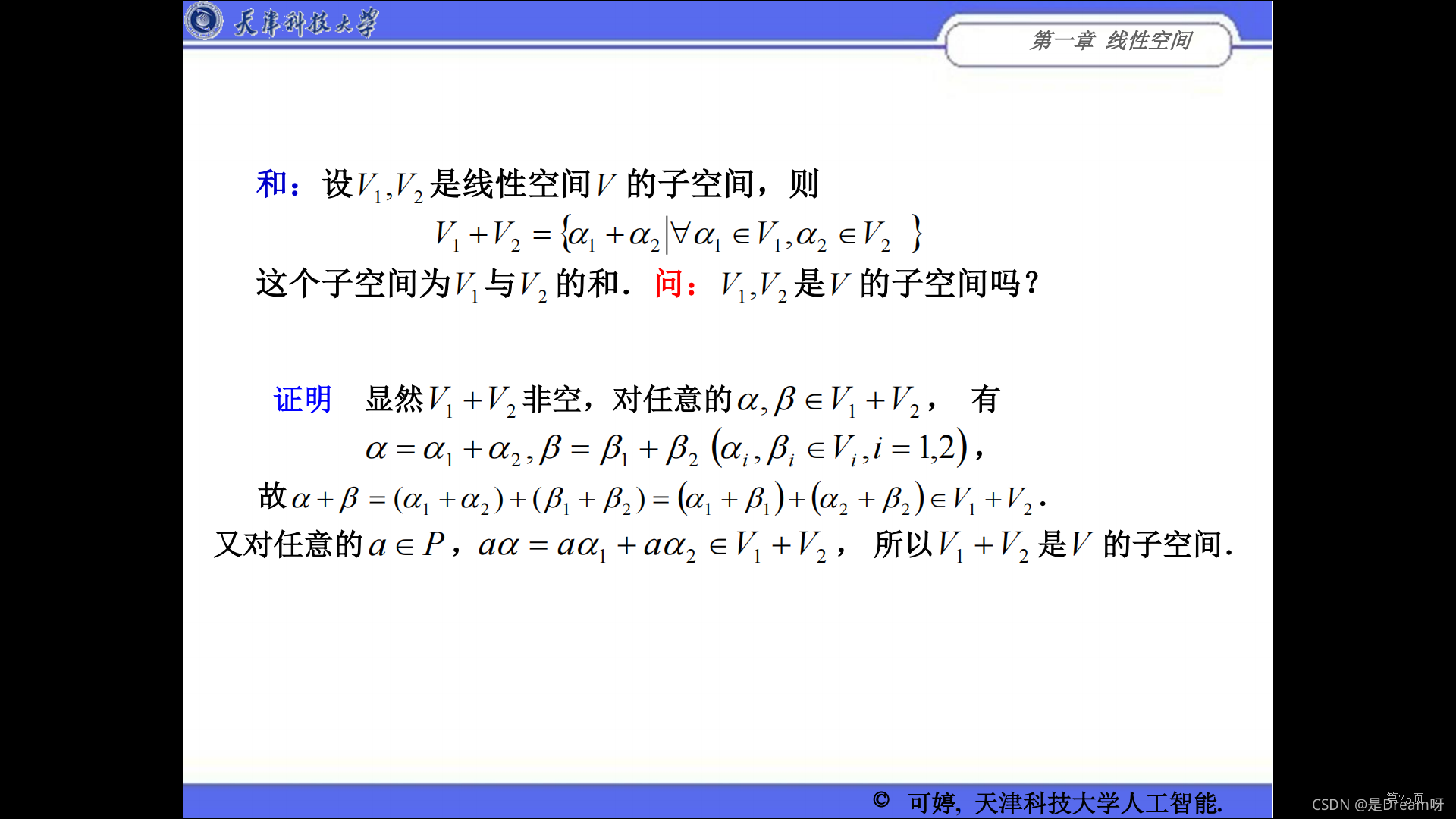
六、子空间的交与和
好啦,这就是今天要分享给大家的全部内容了
❤️❤️❤️如果你喜欢的话,就不要吝惜你的一键三连了~


本文摘自 :https://blog.51cto.com/u

