角点匹配的通用流程:提取检测子,筛选后生成描述子,特征点匹配,去除匹配错误点
Sift角点提取:
1、高斯模糊
高斯模糊(图像和高斯核卷积得到的结果),对图像进行一定的平滑处理。其中sigma表示的是尺度空间,它表示的是图像模糊的程度,值越大图像越模糊,越小越接近原图。
2、构建高斯金字塔
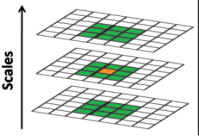
(1) 先将原图像扩大一倍之后作为高斯金字塔的第1组第1层,将第1组第1层图像经高斯卷积(其实就是高斯平滑或称高斯滤波)之后作为第1组金字塔的第2层,然后将sigma乘以一个比例系数k,等到 一个新的平滑系数,用它来平滑第1组第2层图像,结果图像作为第3层。重复操作,最后得到L层图像,在同一组中,每一层图像的尺寸都是一样的,只是平滑系数不一样,由于高斯系数不同,导致尺度空间(看一张图像的纵深,离得近看得清楚,离得远看的模糊)也不同,sift要找的就是在不同尺度空间都存在的极值点。
(2) 用第1组倒数第三层图像做一倍降采样,得到的图像作为第2组的第1层,然后对第2组的第1层图像做平滑因子为sigma的高斯平滑,依次类推得到第2组
(3) 以此类推得到N组不同的高斯差分图,他们的区别是每组之间大小差一倍。然后对同一组的图进行差分,得到高斯差分图,因此得到N组尺寸不同的差分图用于后续提取特征
3、选取特征点
有了高斯差分后的图像后就是要寻找极值点了。极值点的检测只在同一组中从第二层开始至倒数第二层为止的相邻层进行Dog(difference of gauss)的极值搜索。用当前获取到候选的极值点与八邻域,以及上一个和下一个高斯尺度进行比较,如果该点是极值则保留。
4、筛选特征点
1、首先上一步选取的极值点本身是离散的,因此需要做子像元插值,也叫亚像素插值(利用离散的点插值到连续空间的点)。
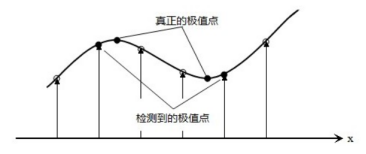
2、在某个尺度下的极值点空间位置为(x,y,σ), 连续情况下,极值点可能落在了(x,y,σ)的附近,设其偏离了(x,y,σ)的坐标为(Δx,Δy,Δσ),因此用D(x)表示在(x,y,σ)点展开
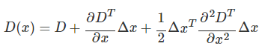
令泰勒展开式倒数为0,求得对应的Δx,Δy,Δσ,经过多次迭代最终得到连续空间极值点对应的值,这里应该是sift的精髓,利用尺度空间的工具,构造了一个利用有限的离散数据来逼近连续的数据
中的极值的方法
3、细化候选极值点:去除较小的极值点;去掉边缘极值点
(1) 插值后的连续空间的点对应的极值,根据一个阈值进行判断是否保 留
(2) 特征点落在边缘比较麻烦,因为有定位歧义,另外容易受到噪声干 扰,边缘在水平方向的梯度比较大,竖直方向梯度比较小,这里通过黑 塞矩阵表示x和y方向的二阶导,求解黑塞矩阵两个
方向梯度值的比值, 如果两个特征值差别越小,越有可能是角点,差别大则可能是边缘,因 此设置一个阈值10作为比值的阈值
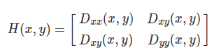
5、生成梯度方向与特征描述
(1) 梯度方向
以当前特征点所在区域,R为半径 这里r = 3 * 1.5 * sigma(高斯尺度),计算该区域所有像素的幅度和幅角
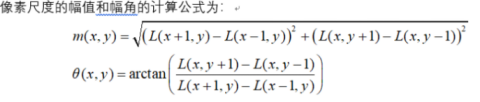
以10度为步长构建360度的直方图,并将该区域幅度统计进去,求出幅度最大的幅角作为主方向,为了得到更精确的角度,通过选取离主峰最近的3个峰做抛物线插值,找到精确的角度。另外,
如果次高幅度达到主幅度的80%,则保留为次方向。到这里每个特征点都包含了(x,y,σ,θ),有次方向的复制为两个特征点
(2) 特征描述
主要步骤为矫正主方向,生成描述子,归一化
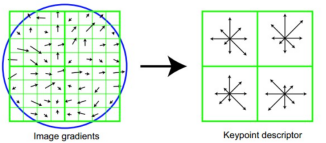
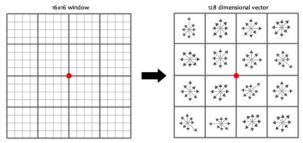
首先以特征点为中心,旋转后将特征点主方向与坐标轴对其,选取以特征点为中心的8x8邻域像素,计算幅度和幅角 ,每个4x4小块儿分别计算其8个方向单位的梯度直方图,作为每个小块儿的
独立特征。在实际实现过程中,sift计算了16x16邻域像素,也就是生成了16个小块,共128维特征。
Surf vs sift:
看过一篇论文对sift和surf的比较,sift对尺度和旋转要优于surf,surf在亮度变化下效果最好,并且速度是sift的3倍
Surf更快:
1、尺度空间构建避开使用高斯核,而是使用不同大小的方框滤波,这样速度更快
(1)方框滤波:利用积分图原理对filter内元素求和
(2)积分图
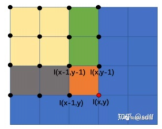
点(x,y)的积分值可以使用点(x-1,y)与点(x,y-1)的积分值之和,然后减去 重叠区域,也就是减去点(x-1,y-1)的积分值,最后再加上点(x,y)的像素 值得到点(x,y)的积分值。
2、统计该区域的harr哈尔小波响应得出主方向
3、以特征点为中心选取一个区域,将其划分为16个正方形,每个正方形内为5x5大小,计算每个正方形针对harr小波响应的 dx, dy, dx绝对值,dy绝对值
角点匹配:FLANN快速最近邻匹配库
先构建KD树对数据进行索引划分,减少暴力穷举法的计算量。然后通过KNN计算该点与模板特征点中的哪个点的距离最近,找到N组匹配对后,用RANSAC进行错误点剔除。
(1)KD树:
减少搜索时间的数据结构,根据超平面进行分割下图所示,是k=2时的一颗kd树。需要提醒的是进行划分(split)的维度的顺序可以是任意的,不一定按照x,y,z,x,y,z…的顺序进行。每一个节点都会
记录划分的维度。FLANN中有划分维度选择的算法。
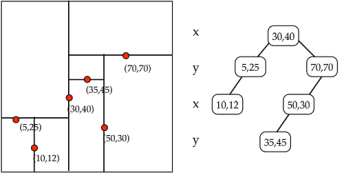
KD树的构建:
KD树是一个二叉树,对数据空间空间进行划分,每一个结点对应一个空间范围。如上图所示,三维空间的划分方式。首先确定在数据集上对应方差最大的维度ki,并找到在ki维度上的数据集的中值kv(并作为根节点),即第一步把空间划分成两部分,在第ki维上小于kv的为一部分称为左子节点,大于kv的为另外一部分对应右子节点,,然后再利用同样的方法,对左子结点和右子节点继续构建二叉树,直所剩数据集为空。
例子:有5个数据,每个数据都是5维,建立KD树。A<7,5,7,3,8>;B<3,4,1,2,7>;C<5,2,6,6,9>;D<9,3,2,4,1>,E<2,1,5,1,4>,首先在计算在5个维度上的方差为6.56;2;5.36;2.96;8.56;可见在第5维度上方差最大,继续在第5个维度上找到中值为7,即B点,在第5维度上值小于7的作为左子树数据(A,C),大于7的作为右子树(D,E),然后继续在A,C,两点上计算方差最大的维度,继续划分。D,E也是如此。
KD树的查询:
从根节点开始沿二叉树搜索,直到叶子结点为止,此时该叶节点并不一定是最近的点,但是一定是叶子结点附近的点。所以一定要有回溯的过程,回溯到根节点为止。也就是所有途径的点中并未被选中的点也会参与计算。
例如:查询与M<5,4,1,3,6>点的最近邻点,查询路径为B,A,C,计算完MC的距离后,逆序向上,查询A及A的右子树,再次回溯B及B左子树,最后得到最近的距离,MB点最近。
Sift改进KD树:
一般来说用标准的KD树时数据集的维数不超过20,但是像SIFT特征描述子128为,SURF描述子为64维,所以要对现有的KD树进行改进。正常回溯的过程,完全是按照查询时路径决定的,没有考虑查询路径上的数据性质。
BBF(Best-Bin-First)查询机制能确保优先包含最近邻点的空间,即BBF维护了一个优先队列,每一次查询到左子树或右子树的过程中,同时计算查询点在该维度的中值的距离差保存在优先队列里,同时另一个孩子节点地址也存入队列里,回溯的过程即从优先队列按(差值)从小到大的顺序依次回溯。BBF设置了超时机制,为了在高维数据上,满足检索速度的需要以精度换取时间,获得快速查询。这样可知,BBF机制找到的最近邻是近似的,并非是最近的,只能说是离最近点比较近而已。
KNN最近邻算法:
首先求测试数据与训练数据的欧式距离,然后根据距离进行升序排序,接下来取前K个数据进行加权平均,根据单个数据占前k个数据距离的比值来综合计算前k个数据的类别,从而判断测试数据的类别。在sift里,每个特征点有128维的特征,根据对模板128维特征的距离进行计算,这里K取1,则距离最小的点则可能是对应的匹配点
RANSAC随机抽样一致:
寻找一个最佳单应性矩阵H,矩阵大小为3×3。RANSAC目的是找到最优的参数矩阵使得满足该矩阵的数据点个数最多。由于单应性矩阵有8个未知参数,至少需要8个线性方程求解,对应到点位置信息上,一组点对可以列出两个方程,则至少包含4组匹配点对。
1、随机从数据集中随机抽出4个样本数据 (此4个样本之间不能共线),计算出变换矩阵H,记为模型M
2、计算数据集中所有数据与模型M的投影误差,若误差小于阈值,加入内点集
3、如果当前内点集 I 元素个数大于最优内点集 I_best , 则更新 I_best = I,同时更新迭代次数k
4、如果迭代次数大于k,则退出 ; 否则迭代次数加1,并重复上述步骤
5、最终只保留内点集中的匹配点对
到这里,整个sift角点提取,匹配,去重的整个流程就结束了,经典永流传
本文摘自 :https://www.cnblogs.com/

