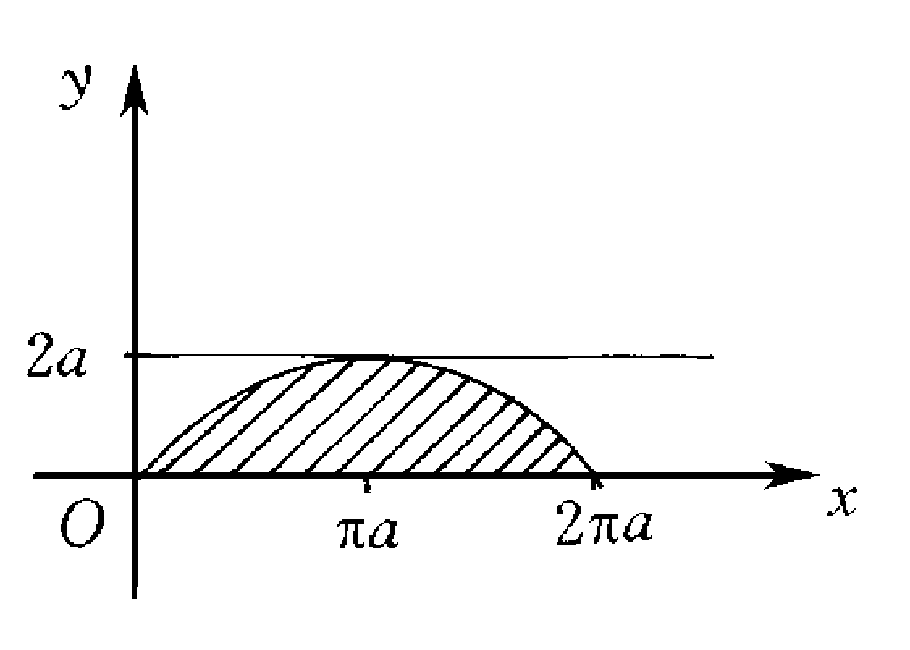
解 作坐标平移变换,即令 x~=x,y~=y-2a.则在新坐标系下,摆线方程成为:x~=a(t-sint) y~=a(1-cost)-2a.直线y=0,成为y~=-2a.并且图形绕直线y=2a旋转所产生立体,即是其在新坐标系下,由曲线x~=a(t-sint),y~=a(1-cost)-2a与直线y~= (本文共 289 字 , 1 张图 ) [阅读本文] >>
海量资源,尽在掌握

解 作坐标平移变换,即令 x~=x,y~=y-2a.则在新坐标系下,摆线方程成为:x~=a(t-sint) y~=a(1-cost)-2a.直线y=0,成为y~=-2a.并且图形绕直线y=2a旋转所产生立体,即是其在新坐标系下,由曲线x~=a(t-sint),y~=a(1-cost)-2a与直线y~= (本文共 289 字 , 1 张图 ) [阅读本文] >>
 说明: 本文档由创作者上传发布,版权归属创作者。若内容存在侵权,请点击申诉举报
说明: 本文档由创作者上传发布,版权归属创作者。若内容存在侵权,请点击申诉举报