APP 
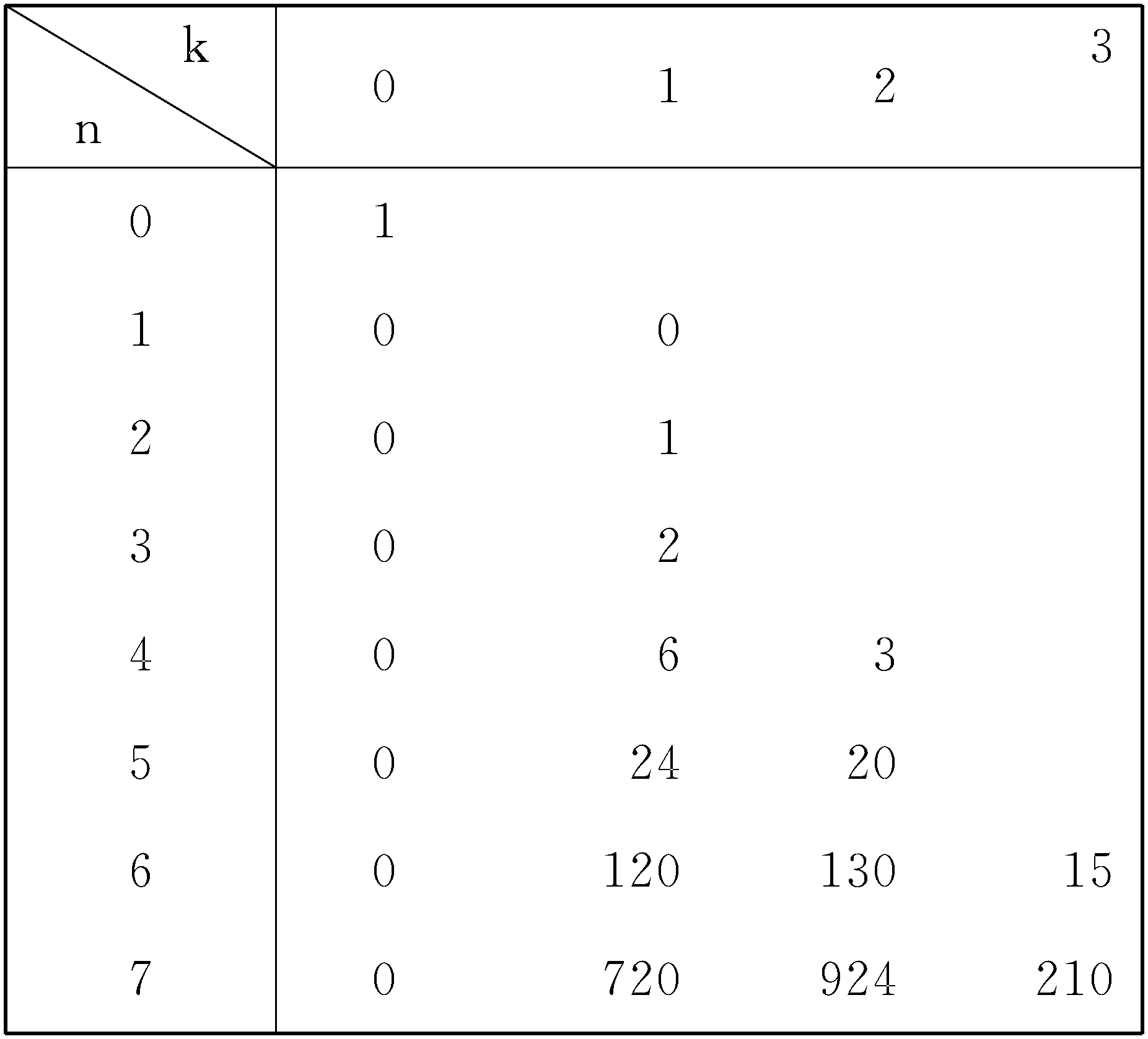
一类组合数.第一类连带斯特林数d(n,k)的组合意义是特殊的n元置换,它具有k个不相交循环,且其中没有一个是单元循环,这样的置换的个数是d(n,k).关于d(n,k),有递归关系d(n+1,k)=nd(n,k)+nd(n-1,k-1).第一类连带斯特林数d(n,k)的值如下表:第二类连 （本文共 234 字 , 2 张图 ） [阅读本文] >>
海量资源，尽在掌握
一类组合数.第一类连带斯特林数d(n,k)的组合意义是特殊的n元置换,它具有k个不相交循环,且其中没有一个是单元循环,这样的置换的个数是d(n,k).关于d(n,k),有递归关系d(n+1,k)=nd(n,k)+nd(n-1,k-1).第一类连带斯特林数d(n,k)的值如下表:第二类连 （本文共 234 字 , 2 张图 ） [阅读本文] >>
说明： 本文档由创作者上传发布，版权归属创作者。若内容存在侵权，请点击申诉举报
