APP 
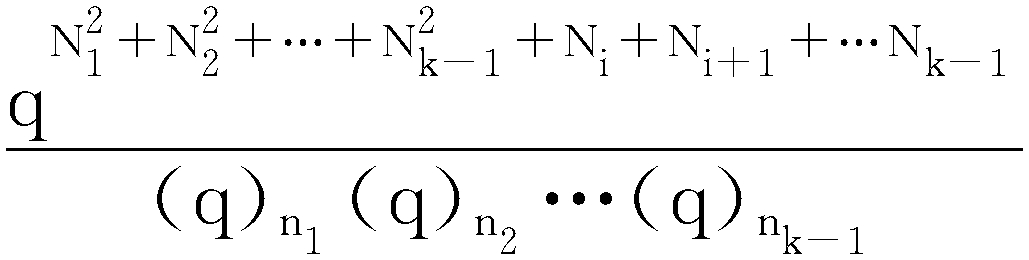
一类组合恒等式.当1≤i≤k,k≥2,|q|<1时 ＝(1-qn)-1,其中Nj＝ni,(q)n＝(1-q)(1-q2)…(1-qn),这就是戈登恒等式.其组合意义如下:若Bk,i(n)表示正整数n的形如下列形式(b1,b2,…,bs),bj-bj+k-1≥2,且至多有i-1个bj等于1的分拆方法数,Ak,i(n)表示将n分拆为 （本文共 218 字 , 3 张图 ） [阅读本文] >>
海量资源，尽在掌握
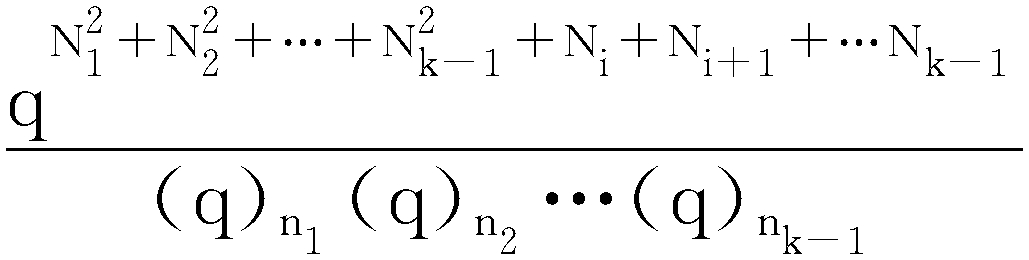
一类组合恒等式.当1≤i≤k,k≥2,|q|<1时 ＝(1-qn)-1,其中Nj＝ni,(q)n＝(1-q)(1-q2)…(1-qn),这就是戈登恒等式.其组合意义如下:若Bk,i(n)表示正整数n的形如下列形式(b1,b2,…,bs),bj-bj+k-1≥2,且至多有i-1个bj等于1的分拆方法数,Ak,i(n)表示将n分拆为 （本文共 218 字 , 3 张图 ） [阅读本文] >>
说明： 本文档由创作者上传发布，版权归属创作者。若内容存在侵权，请点击申诉举报
