证 显然f(x)>0,x∈(-∞,+∞).当|x|≤1时,≤1+x2≤2;当|x|≥1时,.故f(x)≤2,ᗄx∈R.由上面第58题知,f(x)在(-∞,+∞)中是有界的....[继续阅读]
海量资源,尽在掌握
 在(-∞,+∞)中有界.
在(-∞,+∞)中有界.
证 显然f(x)>0,x∈(-∞,+∞).当|x|≤1时,≤1+x2≤2;当|x|≥1时,.故f(x)≤2,ᗄx∈R.由上面第58题知,f(x)在(-∞,+∞)中是有界的....[继续阅读]
答 (1)2π. (2). 因T=....[继续阅读]
答 (1)2. 因T==2.(2)π. 因y=sin2x=-cos2x+,所以T==π....[继续阅读]
证 (1)用反证法. 设[x]的周期为T>0.并设[T]=m≥0.令x=1-a,那么,当m=0时,T=a,其中0<a<1.[T+x]=[T+(1-a)]=1,而[x]=[1-a]=0,于是有[T+x]≠[x].当m>0时,[T+1]=m+1,而[1]=1,也有[T+1]≠[1].矛盾.故证明了[x]不是周期函数.(2)令f(x)=[x]-x,f(1+x)=[1+x]-(1+x)=1+[x]-...[继续阅读]
证 f[x+2(b-a)]=f[b+(x+b-2a)]=f[b-(x+b-2a)]=f(2a-x)=f[a+(a-x)]=f[a-(a-x)]=f(x).故f(x)是以2b-2a为周期的周期函数....[继续阅读]
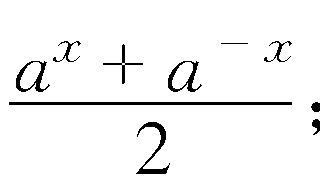
 (5) y=3x2-x3;(6) y=x(x-1)(x+1);
(5) y=3x2-x3;(6) y=x(x-1)(x+1);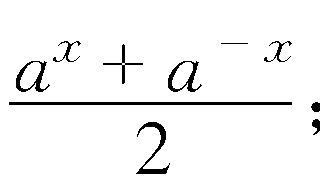
答 是偶函数的有(2),(4),(8),(10).是奇函数的有(3),(6),(9).既是奇函数又是偶函数的有(1).非奇非偶函数有(5),(7)....[继续阅读]
解 φ(x)=[f(x)+f(-x)]=2x2-3,ψ(x)=[f(x)-f(-x)]=6x.所以,φ(x)是偶函数,ψ(x)是奇函数....[继续阅读]
证 (1)设f1(x),f2(x)均为偶函数,令F(x)=f1(x)+f2(x),因F(-x)=f1(-x)+f2(-x)=f1(x)+f2(x)=F(x),故F(x)为偶函数.设g1(x),g2(x)均为奇函数,令G(x)=g1(x)+g2(x),因G(-x)=g1(-x)+g2(-x)=-g1(x)-g2(x)=-G(x),故G(x)为奇函数.(2)设f1(x),f2(x)均为偶函数,令F(x)=f1(x)·f2(x),因F(-x)=f1(-x)·...[继续阅读]
答 B. 因f(4)=f(-1+5)=f(-1)=1,故选B....[继续阅读]
 之间的大小顺序是( )
之间的大小顺序是( )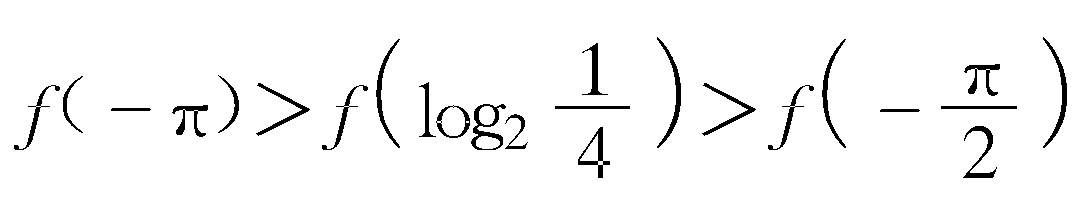
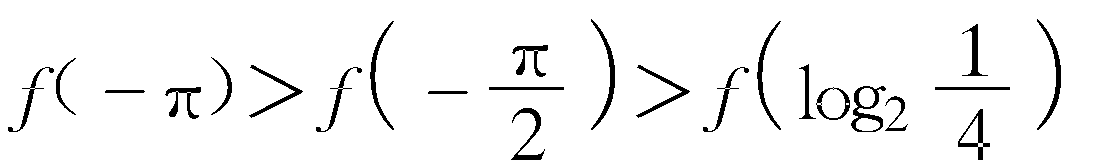
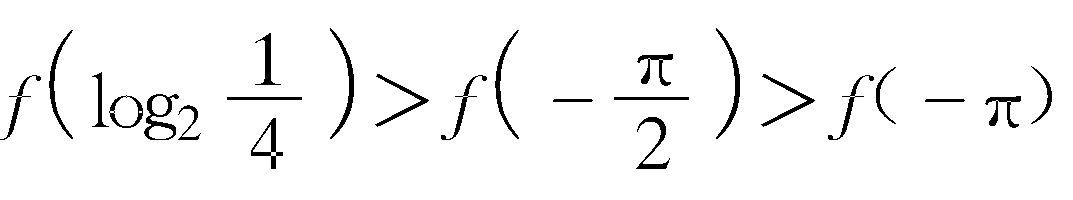
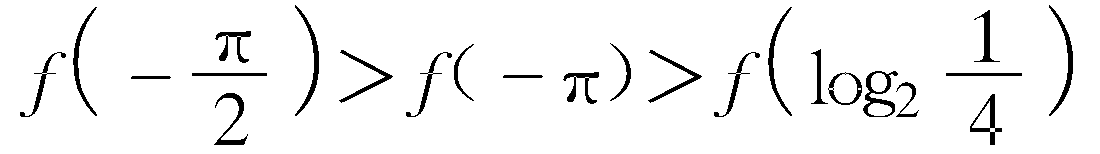 ">81. 已知偶函数f(x)在[0,π]上是增函数,那么f(-π),f
">81. 已知偶函数f(x)在[0,π]上是增函数,那么f(-π),f ,f
,f 之间的大小顺序是( )
之间的大小顺序是( )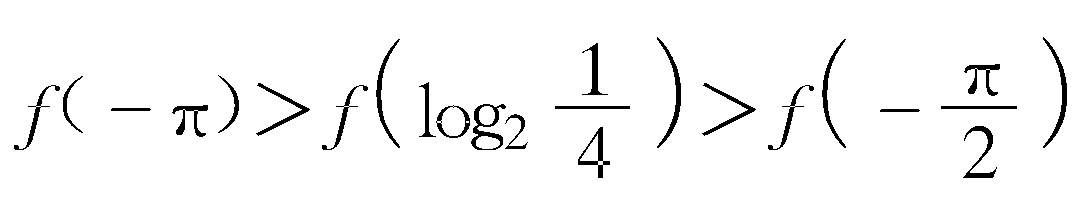
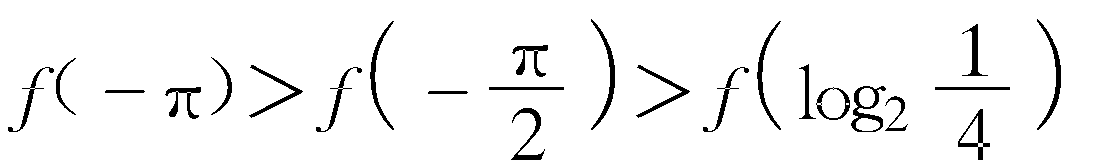
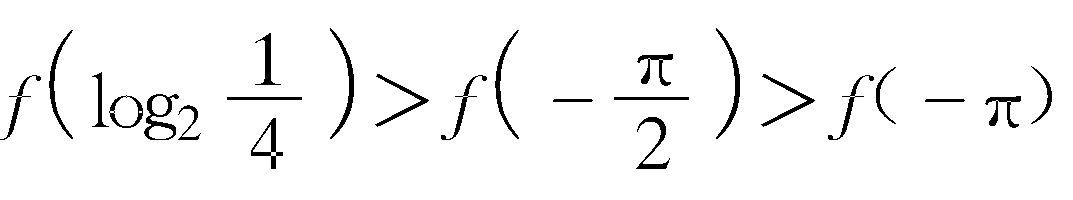
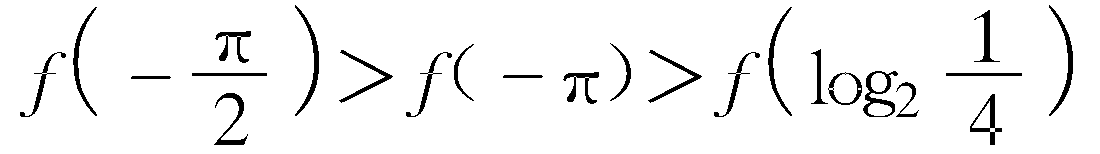
答 A. 因为log2=-2,且偶函数f(x)在[0,π]上是增函数,则f(x)在[-π,0]上是减函数.又-π<-2<-,故f(-π)>f>f.故选A....[继续阅读]