APP 解 AB=DC=,由S0＝h(2BC+2cot40°·h),得BC=-cot40°·h.故自变量h的取值由不等式组确定.故函数定义域D=｛h|0<h<｝.(第48题图)...[继续阅读]
高等数学
字数： 92
海量资源，尽在掌握
解 AB=DC=,由S0＝h(2BC+2cot40°·h),得BC=-cot40°·h.故自变量h的取值由不等式组确定.故函数定义域D=｛h|0<h<｝.(第48题图)...[继续阅读]
解 由△SAO∽△SCB,得.设SC=h,则,得设圆锥体积为V,则自变量h的取值由不等式组确定,故函数定义域D=｛h|2r<h<+∞｝.(第49题图)...[继续阅读]
解 函数关系式如下:(第50题图)...[继续阅读]
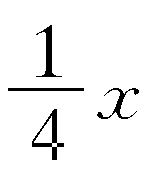在第1象限内所围成的平面图形，并求出它们的交点坐标；(3) 确定出y=x，x2+y2">52. (1) 确定直线x+y=1，y=x，x=0所围成的平面图形，并求出它们的交点坐标；(2) 确定y=
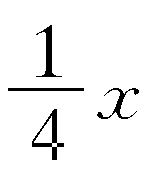，y=x，y=在第1象限内所围成的平面图形，并求出它们的交点坐标；(3) 确定出y=x，x2+y2
解 (1)设此平面图形为D1,它由第52题(1)图所示,(2)设此平面图形为D2,它由第52题(2)图所示.它的三个交点为:O(0,0),P(1,1),Q.(第52(2)题图)(第52(3)题图)(3)设此平面图形为D3,它由第52题(3)图所示.它们交点由方程组⇒x2-x=0⇒x=0或x=1⇒...[继续阅读]
答 设函数f(x)的定义域为D,数集X⊂D,若存在数A(或B)使得f(x)≤A (或f(x)≥B),ᗄx∈X成立,则称f(x)在X上有上(或下)界,若存在正数M,使得|f(x)|≤M, ᗄx∈X成立,则称f(x)在X上有界,如果这样的M不存在,则称f(x)在X上无界. 注 (1)有...[继续阅读]
答 设函数f(x)的定义域为D,区间I⊂D.如果ᗄx1,x2∈I,且x1<x2时,恒有f(x1)<f(x2),则称f(x)在区间I上是单调增加的.如果ᗄx1,x2∈I,且x1<x2时,恒有f(x1)>f(x2),则称f(x)在区间I上是单调减少的.单调增加和单调减少的函数统称为单...[继续阅读]
答 设函数f(x)的定义域D关于原点对称,如果对于ᗄx∈D,都有f(-x)=f(x)成立,则称f(x)为偶函数.如果对于ᗄx∈D,都有f(-x)=-f(x)成立,则称f(x)为奇函数.偶函数的图形关于y轴对称;奇函数的图形关于原点对称....[继续阅读]
答 设函数f(x)的定义域为D,如果存在一个不为零的数l,使得对于ᗄx∈D,有(x±l)∈D,且f(x+l)=f(x)成立,则称f(x)为周期函数,l称为f(x)的周期.通常周期函数的周期是指最小正周期....[继续阅读]
答 不一定.例如f(x)=tanx,g(x)=cotx,φ(x)=-tanx在内都无界,但f(x)·g(x)=1和f(x)+φ(x)=0在内都是有界的....[继续阅读]
证 必要性是显然的.充分性 由于f(x)在X上既有上界又有下界,故对任意x∈X,存在k1,k2,使得f(x)≤k1,f(x)≥k2.取M=max｛|k1|,|k2|｝,则对任意x∈X,有|f(x)|≤M,从而f(x)在X上有界....[继续阅读]